Question

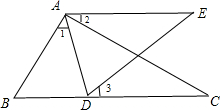如图，在△ABC中，点D为BC边上一点，∠1=∠2=∠3，AC=AE．若AE∥BC，且∠E=∠CAD，求∠C的度数．

Answer 1

考点：等腰三角形的性质,平行线的性质

专题：

分析：由∠1=∠2=∠3，可得∠1+∠DAC=∠DAC+∠2，即∠BAC=∠DAE，又∠1+∠B=∠ADE+∠3，则可得∠B=∠ADE，已知AC=AE，根据AAS证得△ABC≌△ADE，得出AB=AD，令∠E=x，则∠ADB=∠ABD=2x，在△ABD中，可得x+2x+2x=180°，解方程即可．

解答：解：∵∠1=∠2=∠3，
∴∠1+∠DAC=∠DAC+∠2，即∠BAC=∠DAE，
又∵∠1+∠B=∠ADE+∠3，
∴∠B=∠ADE．
在△ABC和△ADE中，

∠BAC=∠DAE ∠B=∠ADE AC=AE

，
∴△ABC≌△ADE（AAS），
∴AB=AD，
∴∠ADB=∠ABD．
∵AE∥BC，
∴∠E=∠3，∠DAE=∠ADB，∠2=∠C，
又∵∠3=∠2=∠1，令∠E=x，
则有：∠DAE=x+x=2x=∠ADB，
∴∠ABD=2x，
∴在△ABD中有：x+2x+2x=180°，
∴x=36°，
∴∠C=∠E=36°．

点评：本题考查了全等三角形的判定与性质，等腰三角形的性质，平行线的性质，三角形内角和定理，难度适中．证明△ABC≌△ADE是解题的关键．