题目内容
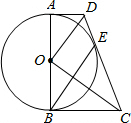 如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,以AB为直径作⊙O,恰与CD相切于点E,连接OD,OC,BE,
如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,以AB为直径作⊙O,恰与CD相切于点E,连接OD,OC,BE,(1)若⊙O的半径为6,AD、BC的长是(x-4)(x-8)=0的两根,求△COD的面积.
(2)求证:OD∥BE.
考点:切线的性质
专题:
分析:(1)连接OE,证出Rt△OAD≌Rt△OED,Rt△COE≌Rt△COB,利用S△COD=S△AOD+S△BOC即可求得△COD的面积.
(2)由Rt△OAD≌Rt△OED,得出∠AOD=∠EOD=
∠AOE,利用同弦对圆周角是圆心角的一半,得出∠ABE=
∠AOE,利用同位角相等两直线平行得到OD∥BE;
(2)由Rt△OAD≌Rt△OED,得出∠AOD=∠EOD=
| 1 |
| 2 |
| 1 |
| 2 |
解答: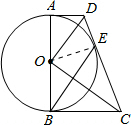 (1)解:如图,连接OE,
(1)解:如图,连接OE,
∵AD∥BC,AD<BC,∠ABC=90°,
∴∠OAD=90°,
∵CD是⊙O的切线,
∴OE⊥CD,
在Rt△OAD和Rt△OED,
,
∴Rt△OAD≌Rt△OED(HL)
同理可证:Rt△COE≌Rt△COB,
∵AD、BC的长是(x-4)(x-8)=0的两根,
∴AD=4,BC=8,
∵OA=OB=6,
∴S△COD=S△AOD+S△BOC=
OA•AD+
OB•BC=
×4×6+
×8×6=36;
(2)证明:∵Rt△OAD≌Rt△OED,
∴∠AOD=∠EOD=
∠AOE,
在⊙O中,∠ABE=
∠AOE,
∴∠AOD=∠ABE,
∴OD∥BE(同位角相等,两直线平行).
 (1)解:如图,连接OE,
(1)解:如图,连接OE,∵AD∥BC,AD<BC,∠ABC=90°,
∴∠OAD=90°,
∵CD是⊙O的切线,
∴OE⊥CD,
在Rt△OAD和Rt△OED,
|
∴Rt△OAD≌Rt△OED(HL)
同理可证:Rt△COE≌Rt△COB,
∵AD、BC的长是(x-4)(x-8)=0的两根,
∴AD=4,BC=8,
∵OA=OB=6,
∴S△COD=S△AOD+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:∵Rt△OAD≌Rt△OED,
∴∠AOD=∠EOD=
| 1 |
| 2 |
在⊙O中,∠ABE=
| 1 |
| 2 |
∴∠AOD=∠ABE,
∴OD∥BE(同位角相等,两直线平行).
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和全等三角形的判定与性质.关键是综合运用,找准线段及角的关系.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.00000065m2.这个数用科学记数法表示为( )mm2.
| A、6.5×10-6 |
| B、0.65×10-6 |
| C、65×10-6 |
| D、6.5×10-7 |
 如图,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠E与∠A的关系.
如图,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠E与∠A的关系. 如图,已知△ABC中,若BC=6,△ABC的面积为12,四边形DEFG是△ABC的内接的正方形,则正方形DEFG的边长是
如图,已知△ABC中,若BC=6,△ABC的面积为12,四边形DEFG是△ABC的内接的正方形,则正方形DEFG的边长是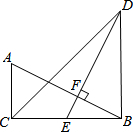 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.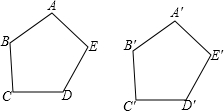 如图,在五边形ABCDE和五边形A1B1C1D1E1中,如果AB=A1B1,BC=B1C1,CD=C1D1,DE=D1E1,EA=E1A1.请添加尽可能少的条件,使它们全等(写出添加的条件,不需要说明理由)
如图,在五边形ABCDE和五边形A1B1C1D1E1中,如果AB=A1B1,BC=B1C1,CD=C1D1,DE=D1E1,EA=E1A1.请添加尽可能少的条件,使它们全等(写出添加的条件,不需要说明理由)