Question

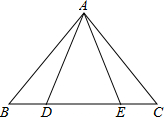如图，等腰三角形ABC中，AB=AC，D、E都在BC上，要使△ABD≌△ACE，需要添加一个条件，某学习小组在讨论这个条件时给出了如下几种方案：
①AD=AE；②BD=CE；③BE=CD；④∠BAD=∠CAE，其中可行的有（　　）

• A、1种
• B、2种
• C、3种
• D、4种

Answer 1

考点：全等三角形的判定

专题：

分析：根据全等三角形的判定定理SAS，ASA，AAS，SSS，对每一个选项进行判断即可．

解答：解：∵在△ABC中，AB=AC，
∴∠B=∠C，
当①AD=AE时，
∴∠ADE=∠AED，
∵∠ADE=∠B+∠BAD，∠AED=∠C+∠CAE，
∴∠BAD=∠CAE，
然后根据SAS或ASA或AAS可判定△ABD≌△ACE；
当②BD=CE时，根据SAS可判定△ABD≌△ACE；
当③BE=CD时，
∴BE-DE=CD-DE，
即BD=CE，根据SAS可判定△ABD≌△ACE；
当④∠BAD=∠CAE时，根据ASA可判定△ABD≌△ACE．
综上所述①②③④均可判定△ABD≌△ACE．
故选D．

点评：本题考查了全等三角形的判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，题目比较好，难度适中．