题目内容
12.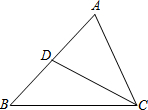 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:(1)△ABC的面积;
(2)sin∠ACD的值.
分析 (1)作AH⊥BC于H,如图,在Rt△ACE中,利用正切的定义得到tan∠ACE=$\frac{AH}{CH}$=3,则设CH=x,AH=3x,根据勾股定理得AC=$\sqrt{10}$x,利用$\sqrt{10}$x=$\sqrt{10}$,解得x=1,再在Rt△ABH中,利用∠B=45°得到BH=AH=3,然后根据三角形面积公式求解;
(2)作DF⊥BC于F,如图,由于CD是AB边上的中线,根据三角形面积公式得到S△ACD=S△ABC=6,再证明DF为△AB的中位线,则DF=$\frac{1}{2}$AH=$\frac{3}{2}$,易得BF=DF=$\frac{3}{2}$,接着根据勾股定理计算出CD=$\frac{\sqrt{34}}{2}$,然后利用锐角三角函数得出sin∠ACD的值.
解答 解:如图,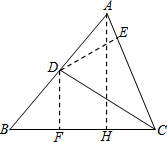
(1)作AH⊥BC于H,
在Rt△ACH中,
∵tan∠ACB=3,AC=$\sqrt{10}$,
设CH=x,AH=3x,
根据勾股定理得AC=$\sqrt{10}$x,
∴CH=1,AH=3,
在Rt△ABH中,∠B=45°,
∴BH=AH=3,
∴S△ABC=$\frac{1}{2}$×4×3=6;
(2)作DF⊥BC于F,
∵S△ACD=$\frac{1}{2}$×$\sqrt{10}$×DE=3,
∴DE=$\frac{3}{5}$$\sqrt{10}$,
∵AH⊥BC,DF⊥BC,CD是AB边上的中线,
∴DF=$\frac{1}{2}$AH=$\frac{3}{2}$,
∴BF=DF=$\frac{3}{2}$,
在Rt△CDF中,CD=$\sqrt{D{F}^{2}+F{C}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+(\frac{5}{2})^{2}}$=$\frac{\sqrt{34}}{2}$,
∴在Rt△CDE中,sin∠ACD=$\frac{DE}{CD}$=$\frac{6\sqrt{85}}{85}$.
点评 此题考查勾股定理的运用,三角函数的意义,三角形的面积计算,以及三角形的中位线定理,正确作出两条垂线是解决问题的关键.

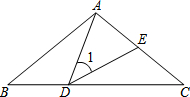 如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.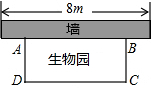 如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米,CD的长为x米.
如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米,CD的长为x米.
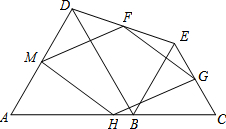 如图,点A、B、C三点在一条直线上,△ABD、△BCE均为等边三角形,连接DE,点F、G、H、M分别为DE、EC、AC、AD的中点.
如图,点A、B、C三点在一条直线上,△ABD、△BCE均为等边三角形,连接DE,点F、G、H、M分别为DE、EC、AC、AD的中点.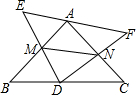 如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N.
如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N.