题目内容
9.菱形的周长为20cm,两个相邻的内角的度数之比为1:2,则较长的对角线的长度是( )| A. | 20 cm | B. | 5$\sqrt{3}$cm | C. | $\frac{5}{2}$$\sqrt{3}$ cm | D. | 5 cm |
分析 根据菱形的性质得出AB=AD=BC=CD=5cm,AD∥BC,AC⊥BD,BD=2BO,AO=OC=$\frac{1}{2}$AC,求出AC=AB=5cm,根据勾股定理求出OB,即可求出答案.
解答 解: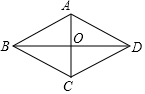
∵菱形的周长为20cm,
∴AB=AD=BC=CD=5cm,AD∥BC,AC⊥BD,BD=2BO,AO=OC=$\frac{1}{2}$AC,
∴∠DAB+∠ABC=180°,
∵两个相邻的内角的度数之比为1:2,
∴∠ABC=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴AC=BC=5cm,
∴AO=$\frac{5}{2}$cm,
在Rt△AOB中,由勾股定理得:BO=$\sqrt{{5}^{2}-(\frac{5}{2})^{2}}$=$\frac{5}{2}$$\sqrt{3}$(cm),
即BD=2OB=5$\sqrt{3}$cm,
故选B.
点评 本题考查了菱形的性质和勾股定理,能灵活运用菱形的性质进行推理是解此题的关键,注意:菱形的对角线互相平分且垂直,菱形的四条边都相等.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
19.下列计算中,正确的是( )
| A. | a3•a2=a6 | B. | $\sqrt{9}$=±6 | C. | ($\frac{1}{2}$)-1=-2 | D. | (π-3.14)0=1 |
20.若a>b,且c为任意有理数,则下列不等式正确的是( )
| A. | ac>bc | B. | ac<bc | C. | ac2>bc2 | D. | a+c>b+c |
14.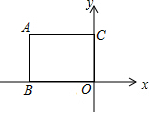 如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
 如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )| A. | (-5,3) | B. | (5,-3) | C. | (-3,5) | D. | (3,-5) |

 如图,已知直线AB∥CD,直线MN分别交AB、CD于点O、P,过点O作OE⊥MN,垂足为点O,若∠BOE=55°,则∠DPN=35°.
如图,已知直线AB∥CD,直线MN分别交AB、CD于点O、P,过点O作OE⊥MN,垂足为点O,若∠BOE=55°,则∠DPN=35°.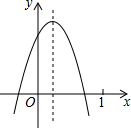 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0.其中正确的是( )