Question

18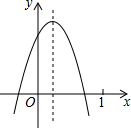．二次函数y=ax²+bx+c（a≠0）的图象如图，则下列结论：①ac＜0；②方程ax²+bx+c=0的两根之和大于0；③y随x的增大而增大；④a-b+c＜0．其中正确的是（　　）

• A． ①②③
• B． ②③④
• C． ①③④
• D． ①②④

Answer 1

分析 根据抛物线的图象开口向下，与y轴的交点在x轴的上方，求出c、a的正负，即可判断①；根据对称轴求出-$\frac{b}{a}$的符号即可判断②；图象被对称轴分成两部分，根据每部分图象的变化情况即可判断③；把x=-1代入抛物线，再根据图象的对称轴位置即可判断④．

解答 解：由图象可知，抛物线开口向下，
∴a＜0，
又∵抛物线与y轴的交点位于y轴坐标轴上，
∴c＞0，
∴ac＜0，故①正确；
∵对称轴x=-$\frac{b}{2a}$＞0，a＜0，
∴b＞0，
∵方程ax²+bx+c=0的两根之和等于-$\frac{b}{a}$，
∴-$\frac{b}{a}$＞0，故②正确；
由图象可知：x$＜-\frac{b}{2a}$时，y随着x的增大而增大，
x＞$-\frac{b}{2a}$时，y随着x的增大而减少，故③错误；
令x=-1，y=a-b+c
由图象可知：a-b+c＜0，故④正确；
故选：D．

点评 本题考查了二次函数的图象与系数的关系的应用，主要考查学生的观察能力和理解能力，二次函数y=ax²+bx+c系数符号与抛物线开口方向、对称轴、与y轴的交点有关．