题目内容
20．若a＞b，且c为任意有理数，则下列不等式正确的是（ ）| A． | ac＞bc | B． | ac＜bc | C． | ac2＞bc2 | D． | a+c＞b+c |
分析 根据不等式的性质进行选择即可．
解答 解：∵a＞b，且c为任意有理数，
∴a+c＞b+c，
故选D．
点评 本题考查了不等式的性质，掌握不等式的性质三条性质是解题的关键．
练习册系列答案
相关题目
10．
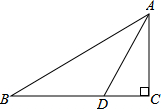如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（ ）
如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（ ）| A． | $\sqrt{3}$-1 | B． | $\sqrt{3}$+1 | C． | $\sqrt{5}$+1 | D． | $\sqrt{5}$-1 |
如图，一条公路两次转弯后，和原来的方向相同．如果第一次的拐角∠A的度数为130°，第二次拐角∠B的度数为130°．
15．
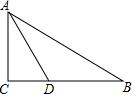如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若BD=4，CD=2，则AC的长是（ ）
如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若BD=4，CD=2，则AC的长是（ ）| A． | 4 | B． | 3 | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$ |
5．
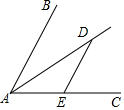如图，∠BAC=60°，AD是∠BAC的角平分线，点D在AD上，过点D作DE∥AB交AC于点E．若DE=2，则点D到AB的距离为（ ）
如图，∠BAC=60°，AD是∠BAC的角平分线，点D在AD上，过点D作DE∥AB交AC于点E．若DE=2，则点D到AB的距离为（ ）| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | 2$\sqrt{3}$ |
299×（-$\frac{1}{2}$）100=$\frac{1}{2}$．
9．菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线的长度是（ ）
| A． | 20 cm | B． | 5$\sqrt{3}$cm | C． | $\frac{5}{2}$$\sqrt{3}$ cm | D． | 5 cm |