题目内容
20.已知反比例函数的图象经过点A(-6,-3).(1)写出函数表达式;
(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?
(3)点B(4,$\frac{9}{2}$)、C(2,-5)在这个函数的图象上吗?
(4)如果点D(a+1,6)在图象上,求a的值.
分析 (1)利用待定系数法可求得反比例函数解析式为y=$\frac{18}{x}$;
(2)根据反比例函数的性质求解;
(3)根据反比例函数图象上点的坐标特征进行判断;
(4)利用反比例函数图象上点的坐标特征得到6(a+1)=18,然后解方程即可.
解答 解:(1)设反比例函数解析式为y=$\frac{k}{x}$,
把A(-6,-3)代入得k=-6×(-3)=18,
所以反比例函数解析式为y=$\frac{18}{x}$;
(2)反比例函数解析式y=$\frac{18}{x}$的图象分布在第一、三象限;
(3)∵4×$\frac{9}{2}$=18,2×(-5)=-10,
∴点B(4,$\frac{9}{2}$)在反比例函数图象上,点C(2,-5)不在这个函数的图象;
(4)把D(a+1,6)代入y=$\frac{18}{x}$得6(a+1)=18,解得a=2.
点评 本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.也考查了反比例函数的性质.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
10. 如图,矩形与⊙O相交,若AB=4,BC=5,DE=3,则EF的长为( )
如图,矩形与⊙O相交,若AB=4,BC=5,DE=3,则EF的长为( )
 如图,矩形与⊙O相交,若AB=4,BC=5,DE=3,则EF的长为( )
如图,矩形与⊙O相交,若AB=4,BC=5,DE=3,则EF的长为( )| A. | 3.5 | B. | 6.5 | C. | 7 | D. | 8 |
9.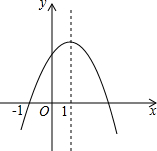 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
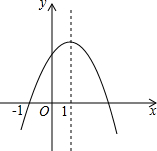 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )| A. | b2-4ac>0 | B. | 当-1<x<3时,y>0 | ||
| C. | c>0 | D. | 当x>1时,y随x的增大而增大 |
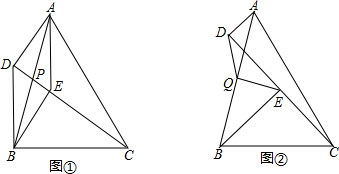
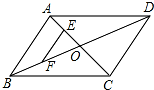 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF=4厘米.
如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF=4厘米.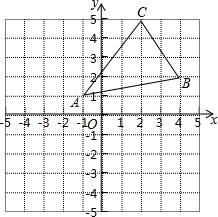 如图,将三角形ABC向左平移3个单位长度,在向下平移4个单位长度,得到三角形A1B1C1.
如图,将三角形ABC向左平移3个单位长度,在向下平移4个单位长度,得到三角形A1B1C1. 如图,Rt△AEF是由Rt△ABC旋转而成的,则旋转中心是点A,旋转角度是∠BAE或∠CAF.
如图,Rt△AEF是由Rt△ABC旋转而成的,则旋转中心是点A,旋转角度是∠BAE或∠CAF.