题目内容
8.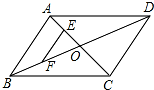 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF=4厘米.
如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF=4厘米.
分析 根据平行四边形的性质可知OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,结合AC+BD=24厘米,△OAB的周长是20厘米,求出AB的长,利用三角形中位线定理求出EF的长.
解答 解:∵?ABCD的对角线AC,BD相交于点O,
∴点O是AC、BD的中点,
∵AC+BD=24厘米,
∴OB+0A=$\frac{1}{2}$(AC+BD)=12厘米,
∵△OAB的周长是20厘米,
∴AB=20-12=8厘米,
∵?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,
∴EF=$\frac{1}{2}$AB=4厘米,
故答案为:4.
点评 本题主要考查了三角形中位线定理以及平行四边形的性质的知识,解答本题的关键是求出AB的长,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.《中华人民共和国个人所得税法》中规定,公民月工薪所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.即全月应纳税所得额=当月工资-3500元.个人所得税款按下表累进计算.
(例如:某人月工资为5500元,需交个人所得税为(5500-3500-1500)×10%+1500×3%=95元)
(1)求月工资为4200元应交的个人所得税款;
(2)设小明的月工资为x元(5000<x<8000),应交的个人所得税为y元,求y与x之间的函数关系式;
(3)若王教授的月工资不超过10000元,他每月的纳税金额超过月工资的$\frac{1}{15}$吗?若能,请给出王教授的工资范围;若不能,请说明理由.
| 全月应纳税金额 | 税率(%) |
| 不超过1500元 | 3% |
| 超过1500元至4500元的部分 | 10% |
| 超过4500元至9000元的部分 | 20% |
| … | … |
(1)求月工资为4200元应交的个人所得税款;
(2)设小明的月工资为x元(5000<x<8000),应交的个人所得税为y元,求y与x之间的函数关系式;
(3)若王教授的月工资不超过10000元,他每月的纳税金额超过月工资的$\frac{1}{15}$吗?若能,请给出王教授的工资范围;若不能,请说明理由.
13. 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )| A. | 22cm | B. | 20cm | C. | 18cm | D. | 16cm |
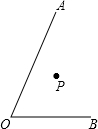 如图,已知∠AOB及∠AOB内部的一点P.
如图,已知∠AOB及∠AOB内部的一点P. 如图,把△ABC绕点C按顺时针方向旋转90°,得到△DEC,AB=2cm,∠ACB=30°,则DE=2cm,∠BCD=60°.
如图,把△ABC绕点C按顺时针方向旋转90°,得到△DEC,AB=2cm,∠ACB=30°,则DE=2cm,∠BCD=60°.