题目内容
9.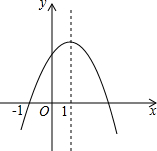 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )| A. | b2-4ac>0 | B. | 当-1<x<3时,y>0 | ||
| C. | c>0 | D. | 当x>1时,y随x的增大而增大 |
分析 A:根据二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个不同的交点,可得△>0,据此判断即可.
B:首先求出函数的图象与x轴的另一个交点是x=3,然后根据函数的图象,可得当-1<x<3时,y>0.
C:根据二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在y轴的正半轴上,可得c>0.
D:根据函数的图象,可得当x>1时,y随x的增大而减小,据此判断即可.
解答 解:∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个不同的交点,
∴△>0,
∴b2-4ac>0,
∴选项A正确;
∵对称轴是x=1,函数的图象与x轴的一个交点是x=-1,
∴函数的图象与x轴的另一个交点是x=3,
∴当-1<x<3时,y>0,
∴选项B正确;
∵二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在y轴的正半轴上,
∴c>0,
∴选项C正确;
∵当x>1时,y随x的增大而减小,
∴选项D不正确.
故选:D.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
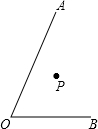 如图,已知∠AOB及∠AOB内部的一点P.
如图,已知∠AOB及∠AOB内部的一点P. 如图,把△ABC绕点C按顺时针方向旋转90°,得到△DEC,AB=2cm,∠ACB=30°,则DE=2cm,∠BCD=60°.
如图,把△ABC绕点C按顺时针方向旋转90°,得到△DEC,AB=2cm,∠ACB=30°,则DE=2cm,∠BCD=60°.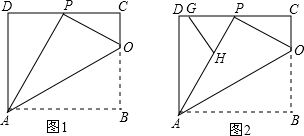
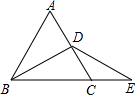 如图,在边长为6cm的等边△ABC中,D是AC的中点,E为BC延长线上一点,若∠DEC=30°,则BE的长为( )cm.
如图,在边长为6cm的等边△ABC中,D是AC的中点,E为BC延长线上一点,若∠DEC=30°,则BE的长为( )cm.