题目内容
17.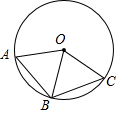 如图,在⊙O中,若∠AOB=∠BOC,则AB=BC,$\widehat{AB}$=$\widehat{BC}$;
如图,在⊙O中,若∠AOB=∠BOC,则AB=BC,$\widehat{AB}$=$\widehat{BC}$;若$\widehat{AB}$=$\widehat{BC}$,则AB=BC,∠AOB=∠BOC;
若AB=BC,则$\widehat{AB}$=$\widehat{BC}$,∠AOB=∠BOC.
分析 直接根据圆心角、弧、弦的关系进行解答即可.
解答 解:在⊙O中,若∠AOB=∠BOC,则AB=BC,$\widehat{AB}$=$\widehat{BC}$;
若$\widehat{AB}$=$\widehat{BC}$,则AB=BC,∠AOB=∠BOC;
若AB=BC,则$\widehat{AB}$=$\widehat{BC}$,∠AOB=∠BOC.
故答案为:AB=BC,$\widehat{AB}$=$\widehat{BC}$;AB=BC,∠AOB=∠BOC;$\widehat{AB}$=$\widehat{BC}$,∠AOB=∠BOC.
点评 本题考查的是圆心角、弧、弦的关系,熟知在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE=100°,EC=2.
如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE=100°,EC=2.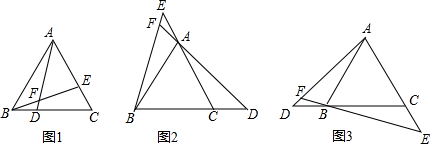
 如图,AB、CD为⊙O的弦,且AB⊥CD,AB将CD分成3cm和7cm两部分,O到弦AB的距离=2cm.
如图,AB、CD为⊙O的弦,且AB⊥CD,AB将CD分成3cm和7cm两部分,O到弦AB的距离=2cm. 如图,在△ABC中,DE是AB的垂直平分线,AE=3cm,△ABC的周长为15cm,则△ACD的周长是9cm.
如图,在△ABC中,DE是AB的垂直平分线,AE=3cm,△ABC的周长为15cm,则△ACD的周长是9cm.