题目内容
12.已知△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且关于x的一元二次方程b(x2-1)-2ax+c(x2+1)=0有两个相等的实数根.①判断△ABC的形状;
②若a=b,求a:b:c的值.
分析 (1)根据已知条件得出△=0,将等式变形,利用勾股定理的逆定理进行判断;
(2)由a=b且a2+b2=c2可得c=$\sqrt{2}$a,即可得答案.
解答 解:(1)∵关于x的一元二次方程(b+c)x2-2ax+c-b=0有两个相等实数根,
∴△=(-2a)2-4(b+c)(c-b)=0,
整理,得a2+b2=c2,
∴△ABC是直角三角形.
(2)若a=b,则c2=2a2,
∴c=$\sqrt{2}$a,
∴a:b:c=1:1:$\sqrt{2}$.
点评 本题考查了根的判别式,勾股定理的逆定理.一元二次方程根的情况与判别式△的关系:(1)△>0,方程有两个不相等的实数根;(2)△=0,方程有两个相等的实数根;(3)△<0,方程没有实数根.

练习册系列答案
相关题目
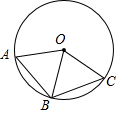 如图,在⊙O中,若∠AOB=∠BOC,则AB=BC,$\widehat{AB}$=$\widehat{BC}$;
如图,在⊙O中,若∠AOB=∠BOC,则AB=BC,$\widehat{AB}$=$\widehat{BC}$; 如图,PA,PB是圆O的切线,切点分别为A,B,若点C位圆O上一点.
如图,PA,PB是圆O的切线,切点分别为A,B,若点C位圆O上一点.