题目内容
17. △ABC中,AD平分∠BAC,AD+BD=AC,∠B=56°,求∠C的度数.
△ABC中,AD平分∠BAC,AD+BD=AC,∠B=56°,求∠C的度数.
分析 延长AB至E,使BE=BD,连接DE,可证明△AED≌△ACD,则可证明△BDE为等腰三角形,再利用外角的性质可求得2∠E=∠ABC=2∠C,可求得答案.
解答 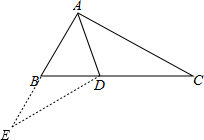 解:
解:
如图,延长AB至E,使BE=BD,连接DE,
∵AD+BD=AC,AE=AB+BE,
∴AE=AC,
又∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△AED和△ACD中
$\left\{\begin{array}{l}{AE=AC}\\{∠EAD=∠CAD}\\{AD=AD}\end{array}\right.$
∴△AED≌△ACD(SAS),
∴∠E=∠C,
∵BD=BE,
∴∠E=∠BDE,
∵∠ABC=∠E+∠BDE=56°,
∴∠E=28°=∠C.
点评 本题主要考查全等三角形的判定和性质,利用条件构造三角形全等是解题的关键.

练习册系列答案
相关题目
8. 如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )
如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )
 如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )
如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )| A. | 5≤a≤12 | B. | 12≤a≤3$\sqrt{17}$ | C. | 12≤a≤4$\sqrt{10}$ | D. | 12≤a≤13 |
9.桌面上摆着一些相同的小正方体木块,从正南方向看如图a,从正西方向看如图b,那么桌面上至少有这样的小正方体木块( )


| A. | 20块 | B. | 16块 | C. | 10块 | D. | 6块 |
 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,求AD•BC的值.
如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,求AD•BC的值. 如图,在2×4的正方形方格中,有格点△ABC(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与△ABC相似但不全等的格点三角形共有( )
如图,在2×4的正方形方格中,有格点△ABC(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与△ABC相似但不全等的格点三角形共有( ) 已知:如图,AD=BC,AC=BD,试证明:∠CAD=∠DBC.
已知:如图,AD=BC,AC=BD,试证明:∠CAD=∠DBC. 如图,在矩形ABCD中截取正方形ABMN,已知MN是BC和CM的比例中项,CM=3-$\sqrt{5}$,求AD的长.
如图,在矩形ABCD中截取正方形ABMN,已知MN是BC和CM的比例中项,CM=3-$\sqrt{5}$,求AD的长.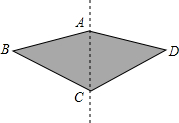 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.