题目内容
4.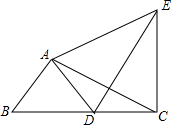 如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.
分析 先利用余弦定义计算出BC=5,再利用勾股定理计算出AC=4,接着根据旋转的性质得AB=AD,AC=AE,∠BAD=∠CAE,利用三角形内角和定理易得∠ACE=∠B,作AH⊥CE于H,由等腰三角形的性质得EH=CH,如图,在Rt△ACH中,利用cos∠ACH=$\frac{CH}{AC}$=$\frac{3}{5}$可计算出CH=$\frac{3}{5}$AC=$\frac{12}{5}$,所以CE=2CH=$\frac{24}{5}$.
解答 解:∵∠BAC=90°,AB=3,cosB=$\frac{AB}{BC}$=$\frac{3}{5}$,
∴BC=5,
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵△ABC绕着点A旋转得△ADE,点B的对应点D落在 边BC上,
边BC上,
∴AB=AD,AC=AE,∠BAD=∠CAE,
∵∠B=$\frac{1}{2}$(180°-∠BAD),∠ACE=$\frac{1}{2}$(180°-∠CAE),
∴∠ACE=∠B,
∴cos∠ACE=cosB=$\frac{3}{5}$,
作AH⊥CE于H,则EH=CH,如图,
在Rt△ACH中,∵cos∠ACH=$\frac{CH}{AC}$=$\frac{3}{5}$,
∴CH=$\frac{3}{5}$AC=$\frac{12}{5}$,
∴CE=2CH=$\frac{24}{5}$.
故答案为$\frac{24}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明∠ACE=∠B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.如图,在“妙手推推推”的游戏中,主持人出示了一个9位数,让参加者猜商品价格.被猜的价格是一个4位数,也就是这个9位中从左到右连在一起的某4个数字.如果参与者不知道商品的价格,从这些连在一起的所有4位数中,任意猜一个,求他猜中该商品价格的概率( )

| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{3}$ |
19.如果x=6是方程2x+3a=6x的解,那么a的值是( )
| A. | 4 | B. | 8 | C. | 9 | D. | -8 |
9.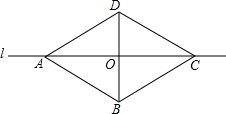 如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
 如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )| A. | ①②③④ | B. | ①③④ | C. | ②③④ | D. | ③④ |
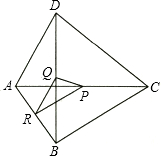 如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.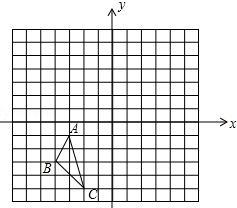 如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).
如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).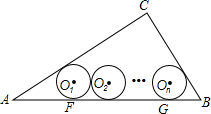 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).