题目内容
14. 如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
分析 由AC⊥AB于点A,BD⊥AB于点B,得到∠A=∠B=90°,推出Rt△ACE≌Rt△BED,根据全等三角形的性质得到∠AEC=∠D,由∠D+∠BED=90°,等量代换得到∠AEC+∠BED=90°,即可得到结论.
解答 证明:∵AC⊥AB于点A,BD⊥AB于点B,
∴∠A=∠B=90°,
在△RtACE和△RtBED中,
$\left\{\begin{array}{l}{AC=BE}\\{CE=DE}\end{array}\right.$,
∴Rt△ACE≌Rt△BED,
∴∠AEC=∠D,
∵∠D+∠BED=90°,
∴∠AEC+∠BED=90°,
∴∠CED=180°-90°=90°,
∴CE⊥DE.
点评 本题考查了全等三角形的判定和性质,垂直的定义,平角的定义,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.若a>b,则下列式子正确的是( )
| A. | a-4>b-3 | B. | $\frac{1}{2}$a<$\frac{1}{2}$b | C. | -3a>-3b | D. | 3+2a>3+2b |
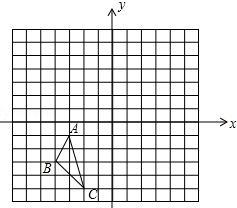 如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).
如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5). 如图所示,△ABC中,∠BAC为锐角,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE交于H,AD=BD.
如图所示,△ABC中,∠BAC为锐角,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE交于H,AD=BD. 已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.
已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE. 在△ABC,∠BAC=90°,AB=AC,AD=DC,AE⊥BD,求证:∠1=∠2.
在△ABC,∠BAC=90°,AB=AC,AD=DC,AE⊥BD,求证:∠1=∠2.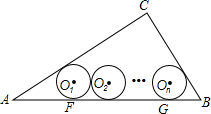 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).