题目内容
2. 如图所示,△ABC中,∠BAC为锐角,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE交于H,AD=BD.
如图所示,△ABC中,∠BAC为锐角,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE交于H,AD=BD.(1)求证:BH=AC;
(2)现将∠BAC改为钝角,按题设要求画出图形,结论BH=AC是否成立?若成立,请证明;若不成立,说明理由.
分析 (1)由直角三角形的性质得出∠HBD=∠DAC,利用ASA证明△BDH≌△ADC,即可得出结论;
(2)同(1)证明△BDH≌△ADC,即可得出结论.
解答 (1)证明:∵AD⊥BC,
∴∠C+∠DAC=90°,
同理:∠C+∠HBD=90°,
∴∠HBD=∠DAC,
在△BDH和△ADC中,$\left\{\begin{array}{l}{∠BDH=∠ADC=90°}&{\;}\\{BD=AD}&{\;}\\{∠HBD=∠DAC}&{\;}\end{array}\right.$,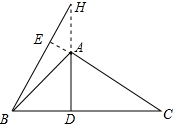
∴△BDH≌△ADC(ASA),
∴BH=AC;
(2)解:成立;理由如下:如图所示:
∵AD⊥BC,BE⊥AC,
∴∠C+∠DAC=90°,∠C+∠HBD=90°,
∴∠HBD=∠C,在△BDH和△ADC中,$\left\{\begin{array}{l}{∠BDH=∠ADC=90°}&{\;}\\{BD=AD}&{\;}\\{∠HBD=∠DAC}&{\;}\end{array}\right.$,
∴△BDH≌△ADC(ASA),
∴BH=AC.
点评 此题主要考查了全等三角形的判定与性质、直角三角形的性质;本题难度适中,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.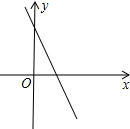 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )| A. | m>n | B. | m<n | C. | m≥n | D. | m≤n |
18. 如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )
如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )
 如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )
如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )| A. | 60° | B. | 50° | ||
| C. | 35° | D. | 条件不够,无法求出 |
 如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,
如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,
 如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.