题目内容
6.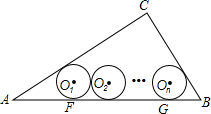 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).
分析 连接AO1,BOn,CO1,COn,O1On,根据△ABC的面积=△AO1 C的面积+△BOnC的面积+△CO1 On的面积+梯形AO1OnB的面积,即可得出结果.
解答 解:连接AO1,BOn,CO1,COn,O1On,如图所示: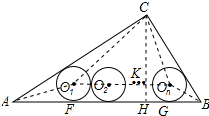
则${S}_{△A{O}_{1}C}=\frac{1}{2}AC•r$=2r,${S}_{△B{O}_{n}C}=\frac{1}{2}BC•r$=$\frac{3}{2}$r
∵等圆⊙O1,⊙O2,…,⊙On依次外切,且均与AB边相切,
∴O1,O2,…,On均在直线O1On上,且O1On∥AB,
∴O1On=(n-2)2r+2r=2(n-1)r.
过点C作CH⊥AB于点H,交O1On于点K,
则CH=$\frac{12}{5}$,CK=$\frac{12}{5}$-r.
${S}_{△C{O}_{1}{O}_{n}}$=$\frac{1}{2}$O1O2•CK=(n-1)($\frac{12}{5}$-r)r,${S}_{梯形A{O}_{1}{O}_{n}B}$=$\frac{1}{2}$[2(n-1)r+5]r=[(n-1)+$\frac{5}{2}$]r,
∵△ABC的面积=△AO1 C的面积+△BOnC的面积+△CO1 On的面积+梯形AO1OnB的面积,
∴6=$\frac{3}{2}$r+2r+(n-1)($\frac{12}{5}$-r)r+[(n-1)r+$\frac{5}{2}$]r,
解得:r=$\frac{5}{2n+3}$,
即这些等圆的半径r=$\frac{5}{2n+3}$.
点评 本题考查了相切两圆的性质、三角形面积的计算方法;解决此题的关键是根据三角形的面积的不同计算方法进行计算.

练习册系列答案
相关题目
15.下列为某两个物体的投影,其中是在太阳光下形成投影的是( )
| A. |  | B. |  | C. |  | D. |  |
16.在平面直角坐标系xOy中,A为双曲线$y=-\frac{6}{x}$上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )
| A. | (-4,$\frac{3}{2}$) | B. | (4,$-\frac{3}{2}$) | C. | (-2,3)或(2,-3) | D. | (-3,2)或(3,-2) |
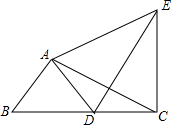 如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$. 如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
如图,已知AC⊥AB于点A,BD⊥AB于点B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.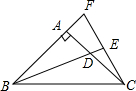 如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系.
如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系. 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: