题目内容
20.先化简,再求值:(1)a3•(-b3)2+(-$\frac{1}{2}$ab2)3,其中a=-$\frac{1}{2}$,b=2
(2)(2x+3)(2x-3)-2x(x+1)-2(x-1)2,其中x=-1.
分析 (1)首先计算乘方,然后进行乘法计算,再合并同类项,最后代入数值计算即可;
(2)首先利用平方差公式以及平方差公式计算,然后去括号、合并同类项即可化简,然后代入数值计算.
解答 解:(1)原式=a3b6-$\frac{1}{8}$a3b6
=$\frac{7}{8}$a3b6,
当a=-$\frac{1}{2}$,b=2时,原式=$\frac{7}{8}$×(-$\frac{1}{2}$)3×26=-7;
(2)原式=4x2-9-2x2-2x-2(x2-2x+1)
=4x2-9-2x2-2x-2x2+4x-2
=2x-11,
当x=-1时,原式=-2-11=-13.
点评 本题考查了整式的化简求值,先按运算顺序把整式化简,再把对应字母的值代入求整式的值.有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似,正确理解乘法公式的结构是关键.

练习册系列答案
相关题目
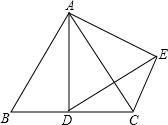 如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,求旋转角度及DE的长.
如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,求旋转角度及DE的长.