题目内容
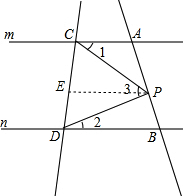
 如图,已知直线m∥n,直线m,n和直线AB分别交于A、B 两点,直线m,n和直线CD分别交于C、D 两点.点P在直线AB上.∠1是线段CP与CA的夹角,∠2是线段DP与DB的夹角,∠3是线段PC与PD的夹角.
如图,已知直线m∥n,直线m,n和直线AB分别交于A、B 两点,直线m,n和直线CD分别交于C、D 两点.点P在直线AB上.∠1是线段CP与CA的夹角,∠2是线段DP与DB的夹角,∠3是线段PC与PD的夹角.(1)如图点P在线段AB上,且不与A,B两点重合.试找出∠1、∠2、∠3之间的关系式,并证明.
(2)如果点P运动到直线m上方时,请画出图形,找出∠1、∠2、∠3之间的关系式,并证明.
(3)如果点P运动到直线n下方时,请画出图形,找出∠1、∠2、∠3之间的关系式,不用证明.
考点:平行线的性质
专题:
分析:作出平行线,利用平行线的性质,两直线平行内错角相等,从而求出∠1、∠2、∠3之间的关系.
(1)过P作PE∥直线m交CD与点E,得到∠2=∠DPE,∠1=∠CPE从而得到∠3=∠1+∠2.
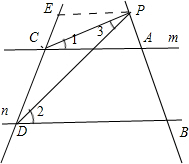
(2)作出图过P作PE∥直线m交CD与E点,∠EPD=∠2,∠CPE=∠1,∠3=∠EPD-∠CPE,即可得出结论.
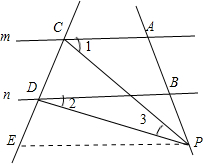
(3)过P作PE∥直线m交CD与E点,∠EPD=∠2,∠EPC=∠1,证得∠3=∠EPC-∠EPD,即可得出结论.
(1)过P作PE∥直线m交CD与点E,得到∠2=∠DPE,∠1=∠CPE从而得到∠3=∠1+∠2.
(2)作出图过P作PE∥直线m交CD与E点,∠EPD=∠2,∠CPE=∠1,∠3=∠EPD-∠CPE,即可得出结论.
(3)过P作PE∥直线m交CD与E点,∠EPD=∠2,∠EPC=∠1,证得∠3=∠EPC-∠EPD,即可得出结论.
解答:解:(1)∠3=∠1+∠2
过P作PE∥直线m交CD与点E
∵直线m∥n
∴PE∥直线n
∴∠2=∠DPE
∵PE∥直线m
∴∠1=∠CPE
又∵∠3=∠DPE+∠CPE
∴∠3=∠1+∠2.
(2)∠3=∠2-∠1
过P作PE∥直线m交CD与E点
∵直线m∥n
∴PE∥直线n
∴∠EPD=∠2
又∵PE∥直线m
∴∠CPE=∠1
∠EPD=∠2
∵∠3=∠EPD-∠EPC
即∠3=∠2-∠1.
(3)∠3=∠1-∠2
过P作PE∥直线m交CD与E点
∵直线m∥n
∴PE∥直线n
∴∠EPD=∠2
又∵PE∥直线m
∴∠EPC=∠1
∵∠3=∠EPC-∠EPD
即∠3=∠1-∠2.
过P作PE∥直线m交CD与点E
∵直线m∥n
∴PE∥直线n
∴∠2=∠DPE
∵PE∥直线m
∴∠1=∠CPE
又∵∠3=∠DPE+∠CPE
∴∠3=∠1+∠2.

(2)∠3=∠2-∠1
过P作PE∥直线m交CD与E点
∵直线m∥n
∴PE∥直线n
∴∠EPD=∠2
又∵PE∥直线m
∴∠CPE=∠1
∠EPD=∠2
∵∠3=∠EPD-∠EPC
即∠3=∠2-∠1.

(3)∠3=∠1-∠2
过P作PE∥直线m交CD与E点
∵直线m∥n
∴PE∥直线n
∴∠EPD=∠2
又∵PE∥直线m
∴∠EPC=∠1
∵∠3=∠EPC-∠EPD
即∠3=∠1-∠2.

点评:主要考查平行线的性质,熟练掌握平行线的性质是解题的关键.

练习册系列答案
相关题目
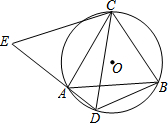 如图,△ABC是⊙O的内接三角形,AC=BC,点D是⊙O中弧AB的上的一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,点D是⊙O中弧AB的上的一点,延长DA至点E,使CE=CD.
 某校开展学年“好书伴我成长”读书活动,为了解全校1500名学生的读书情况,随机调查了部分学生读数的册数,统计数据如下表所示,并绘制了如下统计图.
某校开展学年“好书伴我成长”读书活动,为了解全校1500名学生的读书情况,随机调查了部分学生读数的册数,统计数据如下表所示,并绘制了如下统计图. 如图,点A在第一象限,B(6,0),AC⊥OB,垂足为点C,双曲线y=
如图,点A在第一象限,B(6,0),AC⊥OB,垂足为点C,双曲线y=