题目内容
6.等腰三角形一腰上的高与另一腰的夹角为32°,则该等腰三角形的底角的度数为61°或29°.分析 分锐角三角形和钝角三角形两种情况,利用等腰三角形的性质和三角形内角和定理即可求出它的底角的度数.
解答  解:在三角形ABC中,设AB=AC,BD⊥AC于D.
解:在三角形ABC中,设AB=AC,BD⊥AC于D.
①若是锐角三角形,∠A=90°-32°=58°,
底角=(180°-58°)÷2=61°;
②若三角形是钝角三角形,∠BAC=32°+90°=122°,
此时底角=(180°-122°)÷2=29°.
所以等腰三角形底角的度数是61°或29°.
故答案为:61°或29°.
点评 本题考查了等腰三角形的性质,考查了直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和,利用分类讨论的思想是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.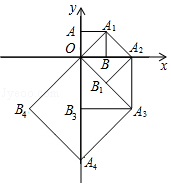 如图,点O(0,0),A(0,1)是正方形的两个顶点,以对角线OA1为边作正方形 OAA1B 再以正方形OA1A2B1的对角线OA2作正方形OA2A3B2,…,依此规律,则点A8的坐标是( )
如图,点O(0,0),A(0,1)是正方形的两个顶点,以对角线OA1为边作正方形 OAA1B 再以正方形OA1A2B1的对角线OA2作正方形OA2A3B2,…,依此规律,则点A8的坐标是( )
 如图,点O(0,0),A(0,1)是正方形的两个顶点,以对角线OA1为边作正方形 OAA1B 再以正方形OA1A2B1的对角线OA2作正方形OA2A3B2,…,依此规律,则点A8的坐标是( )
如图,点O(0,0),A(0,1)是正方形的两个顶点,以对角线OA1为边作正方形 OAA1B 再以正方形OA1A2B1的对角线OA2作正方形OA2A3B2,…,依此规律,则点A8的坐标是( )| A. | (-8,0) | B. | (0,8) | C. | (0,8$\sqrt{2}$) | D. | (0,16) |
15.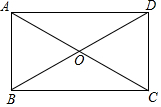 如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )
如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )
如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2cm |
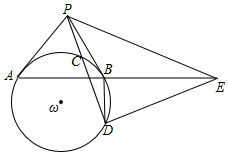 如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB.
如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB. 如图,二次函数y=ax2+bx+c的图象如图,则点P(a,-$\frac{c}{b}$)在第三象限.
如图,二次函数y=ax2+bx+c的图象如图,则点P(a,-$\frac{c}{b}$)在第三象限.