题目内容
7.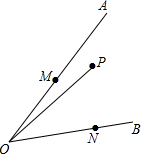 如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运运,若∠AOB=45°,OP=2$\sqrt{2}$,则△PMN的周长的最小值为4.
如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运运,若∠AOB=45°,OP=2$\sqrt{2}$,则△PMN的周长的最小值为4.
分析 作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.
解答 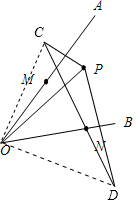 解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.
解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.
∵PC关于OA对称,
∴∠COP=2∠AOP,OC=OP
同理,∠DOP=2∠BOP,OP=OD
∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD.
∴△COD是等腰直角三角形.
则CD=$\sqrt{2}$OC=$\sqrt{2}$×2$\sqrt{2}$=4.
故答案是:4.
点评 本题考查了对称的性质,正确作出图形,理解△PMN周长最小的条件是解题的关键.

练习册系列答案
相关题目
15.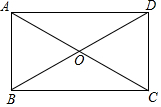 如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )
如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )
如图,在矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,BD=8cm,则CD的长度为( )| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2cm |
19.若m=32,n=43,则126的值(用舍m、n的式子表示)为( )
| A. | mn | B. | m2n2 | C. | m2n3 | D. | m3n2 |
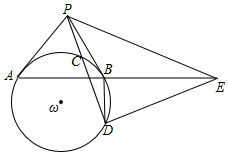 如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB.
如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB. 如图,二次函数y=ax2+bx+c的图象如图,则点P(a,-$\frac{c}{b}$)在第三象限.
如图,二次函数y=ax2+bx+c的图象如图,则点P(a,-$\frac{c}{b}$)在第三象限.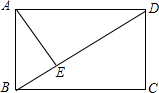 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6.求矩形ABCD的长和宽.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6.求矩形ABCD的长和宽.