题目内容
13．如果$\sqrt{x}$+$\sqrt{y}$=2$\sqrt{3}$，x-y=6，那么$\sqrt{x}-\sqrt{y}$的值是$\sqrt{3}$．分析 由x-y=（$\sqrt{x}$+$\sqrt{y}$）（$\sqrt{x}$-$\sqrt{y}$）=6，再除以$\sqrt{x}$+$\sqrt{y}$，化简得出答案即可．
解答 解：∵x-y=（$\sqrt{x}$+$\sqrt{y}$）（$\sqrt{x}$-$\sqrt{y}$）=6，$\sqrt{x}$+$\sqrt{y}$=2$\sqrt{3}$，
∴$\sqrt{x}-\sqrt{y}$=$\frac{6}{2\sqrt{3}}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．
点评 此题考查二次根式的化简求值，利用平方差公式把式子分解是解决问题的关键．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
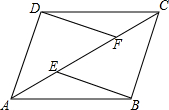如图，在四边形ABCD中，BE=DF．
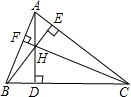如图，△ABC的三条高AD，BE，CF相交于点H．
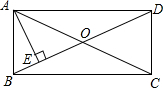如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作BD的垂线，垂足为E，已知∠EAD=3∠BAE，求∠EAD的度数．