题目内容
1.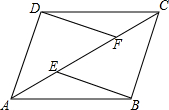 如图,在四边形ABCD中,BE=DF.
如图,在四边形ABCD中,BE=DF.(1)若BC=DA,AE=CF,试判断△ADF与△CBE是否全等,请说明理由;
(2)若AB=CD,AF=CE,试判断△ABE与△CDF是否全等,请说明理由.
分析 (1)由AE=CF,得到AF=CE,根据全等三角形的判定定理“SSS”即可得到结论;
(2)由AF=CE,得到AE=CF,根据全等三角形的判定定理“SSS”即可得到结论.
解答 解:(1)△ADF与△CBE全等,
理由:∵AE=CF,
∴AE+EF=CF+EF,
即:AF=CE,
在△ADF与△CBE中,$\left\{\begin{array}{l}{AD=BC}\\{DF=BE}\\{AF=CE}\end{array}\right.$,
∴△ADF≌△CBE;
(2)△ABE与△CDF全等,
理由:∵AF=CE,
∴AF-EF=CE-EF,
即:AE=CF,
在△ABE与△CDF中,$\left\{\begin{array}{l}{AB=CD}\\{BE=DF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CDF.
点评 本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目