题目内容
如图,数轴上点A、C对应的数分别为a、c,且a、c,满足|a+4|+(c-1)2014=0,点O对应的数为0,点B对应的数为-3.

(1)求数a、c的值;
(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,几秒后,点A追上点B;
(3)在(2)的条件下,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.

(1)求数a、c的值;
(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,几秒后,点A追上点B;
(3)在(2)的条件下,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.
考点:一元一次方程的应用,数轴
专题:
分析:(1)根据非负数的和为0的定理建立方程求出其解;
(2)可设x秒后,点A追上点B,根据等量关系:路程差=速度差×时间,列出方程求解即可;
(3)根据A,B两点到原点O的距离相等分两种情况:当A、B在原点的左侧A、B相遇时和A、B在原点的异侧时,建立方程求出其解即可.
(2)可设x秒后,点A追上点B,根据等量关系:路程差=速度差×时间,列出方程求解即可;
(3)根据A,B两点到原点O的距离相等分两种情况:当A、B在原点的左侧A、B相遇时和A、B在原点的异侧时,建立方程求出其解即可.
解答:解:(1)由题意,得
a+4=0,c-1=0,
解得:a=-4,c=1.
答:a的值是-4,b的值是1;
(2)∵点B对应的数为-3,A对应的数是-4,
∴AB=1,AO=4,BO=3.
设x秒后,点A追上点B,依题意有
2t-t=1,
解得t=1;
(3)∵点B对应的数为-3,A对应的数是-4,
∴AB=1,AO=4,BO=3.
当A、B在原点的左侧A、B相遇时,
2t-t=1,
t=1,
当A、B在原点的异侧时,
2t-4=3-t,
解得:t=
.
∴A,B两点到原点O的距离相等时,t的值为1或
.
a+4=0,c-1=0,
解得:a=-4,c=1.
答:a的值是-4,b的值是1;
(2)∵点B对应的数为-3,A对应的数是-4,
∴AB=1,AO=4,BO=3.
设x秒后,点A追上点B,依题意有
2t-t=1,
解得t=1;
(3)∵点B对应的数为-3,A对应的数是-4,
∴AB=1,AO=4,BO=3.
当A、B在原点的左侧A、B相遇时,
2t-t=1,
t=1,
当A、B在原点的异侧时,
2t-4=3-t,
解得:t=
| 7 |
| 3 |
∴A,B两点到原点O的距离相等时,t的值为1或
| 7 |
| 3 |
点评:本题考查了一元一次方程的运用,数轴的运用,绝对值的运用,偶次幂的运用,解答时根据行程问题的追击问题的数量关系建立方程是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |
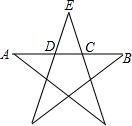 如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.
如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.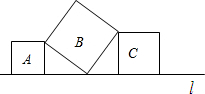 如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为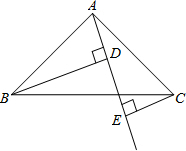 如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.