题目内容
7.计算题(1)(-24x3y2+8x2y3-4x2y2)÷(-2xy)2
(2)-p8•(-p2)3•[(-p)3]2
(3)${(2x-\frac{1}{2}y)^2}{(2x+\frac{1}{2}y)^2}$
(4)(2a-b+3c)2-(3c+b-2a)2
(5)${(-\frac{1}{2})^{-3}}-{2^{100}}×{0.5^{100}}×{(-1)^{2014}}÷{(-1)^{-5}}$
(6)(x-2y+z)(x+2y-z)
分析 (1)根据多项式除以单项式法则计算即可;
(2)先计算各幂的乘方,再计算同底数幂相乘可得;
(3)根据积的乘方转化为平方差公式计算,再计算乘方即可;
(4)利用平方差公式因式分解,再计算两整式的积;
(5)根据实数的混合运算顺序计算即可;
(6)先利用平方差公式计算,再用完全平方公式展开可得.
解答 解:(1)原式=(-24x3y2+8x2y3-4x2y2)÷(4x2y2)=-6x+2y-1;
(2)原式=-p8•(-p6)•p6=p20;
(3)原式=[(2x-$\frac{1}{2}y$)(2x+$\frac{1}{2}y$)]2
=(4x2-$\frac{1}{4}$y2)2
=16x4-2x2y2+$\frac{1}{16}$y4;
(4)原式=(2a-b+3c+3c+b-2a)(2a-b+3c-3c-b+2a)
=6c(4a-2b)
=24ac-12bc;
(5)原式=-8-(2×0.5)100×1÷(-1)
=-8-(-1)
=-7;
(6)原式=[x-(2y-z)][x+(2y-z)]
=x2-(2y-z)2
=x2-(4y2-4yz+z2)
=x2-4y2+4yz-z2.
点评 本题主要考查整式的混合运算,熟练掌握整式的运算法则和平方差公式、完全平方公式是解题根本和关键.

练习册系列答案
相关题目
15.下列实数是无理数的是( )
| A. | -$\sqrt{5}$ | B. | 0 | C. | $\frac{1}{3}$ | D. | 6 |
 如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°.
如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°. 如图,在周长为40cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为20cm.
如图,在周长为40cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为20cm.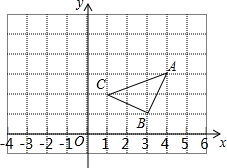 平面直角坐标系中的三是角形ABC如图所示,若三角形A1B1C1是由三角形ABC平移后得到的,且三角形ABC中的任意一点P(x,y)经过平移后的对应点为P1(x-3,y-5),
平面直角坐标系中的三是角形ABC如图所示,若三角形A1B1C1是由三角形ABC平移后得到的,且三角形ABC中的任意一点P(x,y)经过平移后的对应点为P1(x-3,y-5),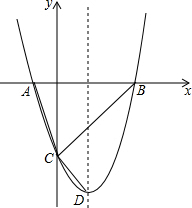 如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.
如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.