题目内容
15．
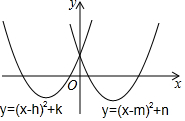图中是有相同最小值的两条抛物线，则下列关系中正确的是（ ）| A． | k＜n | B． | h=m | C． | k+n=0 | D． | h＜0，m＞0 |
分析 根据顶点的位置确定正确的选项即可．
解答 解：∵两条抛物线具有相同的最小值，
∴k=n，
∵顶点分别位于三和四象限，
∴h＜0，m＞0，
故选D．
点评 本题考查了二次函数的最值的知识，解题的关键是能够根据顶点的位置确定h和m的符号，难度不大．
练习册系列答案
相关题目
5．已知抛物线y=ax2+bx+c（a＜0）过A（-4，1），B（0，1），C（x1，y1），D（x2，y2）四点，且y1＜y2，则x1与x2的取值可能是（ ）
| A． | x1=-1，x2=1 | B． | x1=-5，x2=1 | C． | x1=3，x2=-3 | D． | x1=1，x2=-6 |
3．下列说法正确的是（ ）
| A． | “任意一个三角形的外角和等于180°”这一事件是不可能事件 | |
| B． | 必然事件发生的概率为0 | |
| C． | 一组数据1，6，3，9，8的极差为7 | |
| D． | “面积相等的两个三角形全等”这一事件是必然事件 |
20．
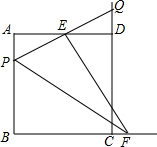在边长为2的正方形ABCD中，P为AB上的一动点，E为AD中点，PE交CD延长线于Q，过E作EF⊥PQ交BC的延长线于F，则下列结论：①△APE≌△DQE；②PQ=EF；③当P为AB中点时，CF=$\sqrt{2}$；④若H为QC的中点，当P从A移动到B时，线段EH扫过的面积为$\frac{1}{2}$，其中正确的是（ ）
在边长为2的正方形ABCD中，P为AB上的一动点，E为AD中点，PE交CD延长线于Q，过E作EF⊥PQ交BC的延长线于F，则下列结论：①△APE≌△DQE；②PQ=EF；③当P为AB中点时，CF=$\sqrt{2}$；④若H为QC的中点，当P从A移动到B时，线段EH扫过的面积为$\frac{1}{2}$，其中正确的是（ ）| A． | ①② | B． | ①②④ | C． | ②③④ | D． | ①②③ |
7．下列各数中，最小的数是（ ）
| A． | 0 | B． | $\frac{π}{3}$ | C． | -$\sqrt{5}$ | D． | -3 |
4．
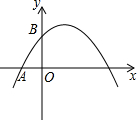如图，抛物线y=-x2+ax+4与x轴负半轴交于点A，与y轴交于点B，且tan∠ABO=$\frac{1}{4}$，点C（x1，y1），D（x2，y2）是抛物线y=-x2+ax+4上两点，当x1≤x≤x2，y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$．则下列结论正确的是（ ）
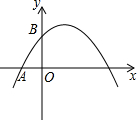如图，抛物线y=-x2+ax+4与x轴负半轴交于点A，与y轴交于点B，且tan∠ABO=$\frac{1}{4}$，点C（x1，y1），D（x2，y2）是抛物线y=-x2+ax+4上两点，当x1≤x≤x2，y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$．则下列结论正确的是（ ）| A． | a=-3 | B． | y2＜4 | C． | |x1-x2|=1 | D． | |x1-$\frac{3}{2}$|＞|x2-$\frac{3}{2}$| |
如图，⊙M的圆心M（-1，2），⊙M经过坐标原点O，与y轴交于点A．经过点A的一条直线l解析式为：y=-$\frac{1}{2}$x+4与x轴交于点B，以M为顶点的抛物线经过x轴上点D（2，0）和点C（-4，0）．