题目内容
17.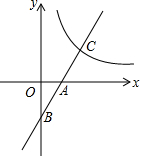 如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
分析 作CD⊥x轴于D,则OB∥CD,易得△AOB∽△ADC,根据相似三角形的性质得出OB=CD=3,根据图象上的点满足函数解析式,把C点纵坐标代入反比例函数解析式,可得横坐标;根据待定系数法,可得一次函数的解析式.
解答 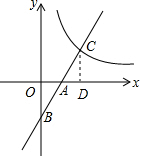 解:作CD⊥x轴于D,则OB∥CD,
解:作CD⊥x轴于D,则OB∥CD,
∴△AOB∽△ADC,
∴$\frac{OB}{CD}$=$\frac{AB}{AC}$,
∵AB=AC,
∴OB=CD,
由直线y=kx-3(k≠0)可知B(0,-3),
∴OB=3,
∴CD=3,
把y=3代入y=$\frac{12}{x}$(x>0)解得,x=4,
∴C(4,3),
代入y=kx-3(k≠0)得,3=4k-3,
解得k=$\frac{3}{2}$,
故答案为$\frac{3}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,图象上的点满足函数解析式,求得C点的坐标是解题的关键.

练习册系列答案
相关题目
8.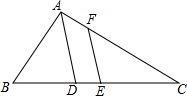 如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
 如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
5.一个n边形的内角和比它的外角和大180°,则n等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.对一组数据:-2,1,2,1,下列说法不正确的是( )
| A. | 平均数是1 | B. | 众数是1 | C. | 中位数是1 | D. | 极差是4 |
6.下列调查中,适合采用全面调查方式的是( )
| A. | 了解一批灯管的使用寿命 | B. | 了解居民对废电池的处理情况 | ||
| C. | 了解一个班级的数学考试成绩 | D. | 了解全国七年级学生的视力情况 |
 如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.
如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.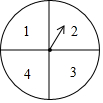 由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负. 如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.
如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.