题目内容
17. 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
分析 ①正确.由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:$\widehat{AD}$=$\widehat{AC}$,DG=CG,继而证得△ADF∽△AED;
②正确.由 $\frac{CF}{FD}$=$\frac{1}{3}$,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;
③错误.由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E=$\frac{\sqrt{5}}{4}$.
④首先求得△ADF的面积,由相似三角形面积的比等于相似比的平方,即可求得△ADE的面积,继而求得S△DEF=4 $\sqrt{5}$.
解答 解:①∵AB是⊙O的直径,弦CD⊥AB,
∴$\widehat{AD}$=$\widehat{AC}$,DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
故①正确;
②∵$\frac{CF}{FD}$=$\frac{1}{3}$,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG-CF=2;
故②正确;
③∵AF=3,FG=2,
∴AG=$\sqrt{A{F}^{2}+F{G}^{2}}$=$\sqrt{5}$,
∴在Rt△AGD中,tan∠ADG=$\frac{AG}{DG}$=$\frac{\sqrt{5}}{4}$,
∴tan∠E=$\frac{\sqrt{5}}{4}$;
故③错误;
④∵DF=DG+FG=6,AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=$\sqrt{21}$,
∴S△ADF=$\frac{1}{2}$DF•AG=$\frac{1}{2}$×6×$\sqrt{5}$=3 $\sqrt{5}$,
∵△ADF∽△AED,
∴$\frac{{S}_{△ADF}}{{S}_{△AED}}$=( $\frac{AF}{AD}$)2,
∴$\frac{3\sqrt{5}}{{S}_{△ADE}}$=$\frac{3}{7}$,
∴S△AED=7 $\sqrt{5}$,
∴S△DEF=S△AED-S△ADF=4 $\sqrt{5}$;
故④正确.
故选C.
点评 此题考查了相似三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | 5 | C. | 6 | D. | 9 |
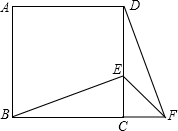 如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )| A. | 15° | B. | 10° | C. | 20° | D. | 25° |
| A. | a+(b-c)=a-b-c | B. | a-(b+c)=a-b-c | C. | m-2(p-q)=m-2p+q | D. | x2-(-x+y)=x2+x+y |
| A. | $\frac{y}{x}$=$\frac{5}{2}$ | B. | $\frac{y}{x}$=$\frac{2}{5}$ | C. | $\frac{x+y}{x}$=$\frac{7}{5}$ | D. | $\frac{x-y}{y}$=$\frac{3}{2}$ |
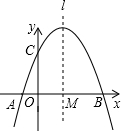 如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.