题目内容
9.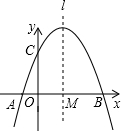 如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.(1)求抛物线的函数的关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求△PAC的周长;
(3)在直线l上是否存在点Q,使以M、O、Q为顶点的三角形与△AOC相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
分析 (1)待定系数法求解可得;
(2)连接BC,交直线l于点P,则此时△PAC的周长最小,先根据点B、C坐标求得直线BC的解析式,再结合直线l的解析式,求得点P的坐标,根据PA+PC+AC=PB+PC+AC=BC+AC,利用勾股定理即可得出答案;
(3)当△AOC∽△OMQ时,根据$\frac{AO}{OM}=\frac{OC}{MQ}$求得MQ的长度可得此时点Q的坐标;当△AOC∽△QMO时,根据$\frac{AO}{QM}=\frac{OC}{MO}$求得MQ的长度可得此时点Q的坐标,继而得出答案.
解答 解:(1)将点A(-1,0)、B(3,0)代入y=ax2+bx+3,得:
$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴y=-x2+2x+3;
(2)如图,连接BC,交直线l于点P,则此时△PAC的周长最小,
∵y=-x2+2x+3中x=0时,y=3,
∴点C坐标为(0,3),
设BC所在直线解析式为y=kx+b,
将点B(3,0)、C(0,3)代入,得:
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为y=-x+3,
又直线l的解析式为x=-$\frac{2}{2×(-1)}$=1,
∴直线l:x=1与直线BC:y=-x+3交点P的坐标为(1,2),
∵点A与点B关于直线l对称,
∴PA=PB,
则PA+PC+AC
=PB+PC+AC
=BC+AC
=$\sqrt{{3}^{2}+{3}^{2}}$+$\sqrt{{1}^{2}+{3}^{2}}$
=3$\sqrt{2}$+$\sqrt{10}$,
即△PAC的周长为3$\sqrt{2}$+$\sqrt{10}$;
(3)存在,
如图2,
∵∠AOC=∠OMQ=90°,
∴当△AOC∽△OMQ时,$\frac{AO}{OM}=\frac{OC}{MQ}$,即$\frac{1}{1}$=$\frac{3}{MQ}$,
则MQ=3,
∴此时点Q的坐标为(1,3)或(1,-3);
当△AOC∽△QMO时,$\frac{AO}{QM}=\frac{OC}{MO}$,即$\frac{1}{QM}$=$\frac{3}{1}$,
则MQ=$\frac{1}{3}$,
∴此时点Q的坐标为(1,$\frac{1}{3}$)或(1,-$\frac{1}{3}$);
综上,点Q的坐标为(1,3)或(1,-3)或(1,$\frac{1}{3}$)或(1,-$\frac{1}{3}$).
点评 本题主要考查待定系数法求函数解析式、相似三角形的判定与性质、轴对称的性质及勾股定理,熟练掌握相似三角形的判定与性质是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 0 | B. | 1 | C. | -1 | D. | 2017 |
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
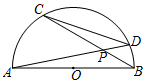 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )| A. | 16:9 | B. | 3:4 | C. | 4:3 | D. | 9:16 |
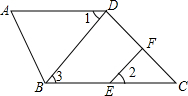 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.