题目内容
12.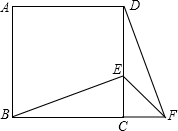 如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )| A. | 15° | B. | 10° | C. | 20° | D. | 25° |
分析 由旋转前后的对应角相等可知,∠DFC=∠BEC=60°;一个特殊三角形△ECF为等腰直角三角形,可知∠EFC=45°,把这两个角作差即可.
解答 解:∵△BCE绕点C顺时针方向旋转90°得到△DCF,
∴CE=CF,∠DFC=∠BEC=60°,∠EFC=45°,
∴∠EFD=60°-45°=15°.
故选:A.
点评 本题考查旋转的性质和正方形的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

练习册系列答案
相关题目
2. 如图,在4×4的网格图中,△ABC的顶点都在格点上,则图中∠BAC的正弦值是( )
如图,在4×4的网格图中,△ABC的顶点都在格点上,则图中∠BAC的正弦值是( )
 如图,在4×4的网格图中,△ABC的顶点都在格点上,则图中∠BAC的正弦值是( )
如图,在4×4的网格图中,△ABC的顶点都在格点上,则图中∠BAC的正弦值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
20.若(a-2)2+|b+3|=0,则(a+b)2017的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2017 |
17. 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
4.设A=x2+1,B=-2x+x2,则2B-3A可化简为( )
| A. | 4x2+1 | B. | -x2-4x-3 | C. | x2-4x-3 | D. | x2-3 |

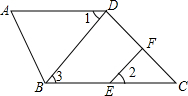 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.