题目内容
13．已知直角平面坐标系内有两点，点P（4，2）与点Q（a，a+2），则PQ的最小值为2$\sqrt{2}$．分析 求直角坐标系内任意两点间的距离可直接套用两点间的距离公式，再根据配方法可求PQ的最小值．
解答 解：∵直角平面坐标系内有两点，点P（4，2）与点Q（a，a+2），
∴PQ=$\sqrt{（a-4）^{2}+（a+2-2）^{2}}$=$\sqrt{2（a-2）^{2}+8}$，
∴当a=2时，PQ的最小值为2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．
点评 考查了两点间的距离公式：设有两点A（x1，y1），B（x2，y2），则这两点间的距离为AB=$\sqrt{（{x}_{1}-{x}_{2}）^{2}+（{y}_{1}-{y}_{2}）^{2}}$．
练习册系列答案
名师点拨卷系列答案
相关题目
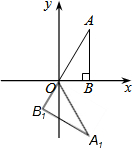如图，已知点A（1，$\sqrt{3}$）、点B（1，0），把△ABO绕点O顺时针旋转120°，得到△A1B1O，则点A1的坐标为（1，-$\sqrt{3}$）．
如图，在△ABC中，AB=AC．
如图，在△ABC，中，∠BAC=90°，沿AD折叠△ABC，使点B恰好落在AC边上的点E处，若∠C=20°，则∠ADE=65°．