题目内容
9. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).
分析 根据一次函数图象上点的坐标特征结合正方形的性质可找出部分点A、B的坐标,根据坐标的变化找出变化规律是解题的关键.(亦可利用等腰直角三角形的性质结合一次函数图象上点的坐标特征找出点An的坐标,进而得出点Bn的坐标)
解答 解:当x=0时,y=x+1=1,
∴A1(0,1).
∵四边形A1B1C1O为正方形,
∴B1(1,1),A2(1,2).
同理可得:B2(3,2),A3(3,4),B3(7,4),A4(7,8),…,
∴An(2n-1-1,2n-1),Bn(2n-1,2n-1)(n为正整数).
故答案为:(2n-1,2n-1)(n为正整数).
点评 本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型中点的坐标,根据点的坐标的变化找出变化规律“An(2n-1-1,2n-1),Bn(2n-1,2n-1)(n为正整数)”是解题的关键.

练习册系列答案
相关题目
17.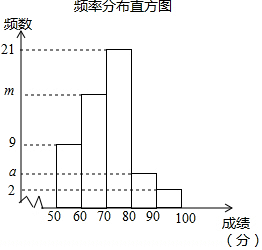 为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、m、n的值;
(2)老师说:“王晓的测试成绩是全班同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)若要从小明、小敏等几位成绩优秀(分数在80≤x≤100范围内为优秀)的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:几位同学请用A、B、C、D…表示,其中小明为A,小敏为B)
 为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:| 组别 | 分组 | 频数 | 频率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | b |
| 3 | 70≤x<80 | 21 | 0.42 |
| 4 | 80≤x<90 | m | 0.06 |
| 5 | 90≤x≤100 | 2 | n |
(2)老师说:“王晓的测试成绩是全班同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)若要从小明、小敏等几位成绩优秀(分数在80≤x≤100范围内为优秀)的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:几位同学请用A、B、C、D…表示,其中小明为A,小敏为B)
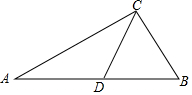 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{\sqrt{2}}{2}$,tanA=$\frac{1}{2}$,AC=3$\sqrt{5}$
如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{\sqrt{2}}{2}$,tanA=$\frac{1}{2}$,AC=3$\sqrt{5}$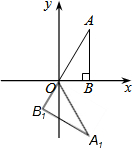 如图,已知点A(1,$\sqrt{3}$)、点B(1,0),把△ABO绕点O顺时针旋转120°,得到△A1B1O,则点A1的坐标为(1,-$\sqrt{3}$).
如图,已知点A(1,$\sqrt{3}$)、点B(1,0),把△ABO绕点O顺时针旋转120°,得到△A1B1O,则点A1的坐标为(1,-$\sqrt{3}$). 如图,在△ABC,中,∠BAC=90°,沿AD折叠△ABC,使点B恰好落在AC边上的点E处,若∠C=20°,则∠ADE=65°.
如图,在△ABC,中,∠BAC=90°,沿AD折叠△ABC,使点B恰好落在AC边上的点E处,若∠C=20°,则∠ADE=65°.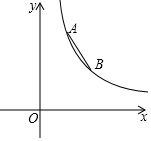 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,且AB=$\sqrt{13}$.则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,且AB=$\sqrt{13}$.则k的值为( )