题目内容
 如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.(1)求证:直线EF是⊙O的切线;
(2)求CD的值.
考点:切线的判定
专题:
分析:根据题意做出辅助线连接OD,CD.
(1)由圆周角定理得∠BDC=90°,等腰三角形的三线合一性质推出∠ACD=∠BCD,根据等边对等角,由OC=OD,推出∠BCD=∠ODC,通过等量代换即可推出∠ODC=∠ACD,得出OD∥AC,根据平行线的性质得出DF⊥AC,从而推出EF与⊙O相切;
(2)由等腰三角形的三线合一性质AD=BD=
AB=6,然后根据勾股定理即可求得CD.
(1)由圆周角定理得∠BDC=90°,等腰三角形的三线合一性质推出∠ACD=∠BCD,根据等边对等角,由OC=OD,推出∠BCD=∠ODC,通过等量代换即可推出∠ODC=∠ACD,得出OD∥AC,根据平行线的性质得出DF⊥AC,从而推出EF与⊙O相切;
(2)由等腰三角形的三线合一性质AD=BD=
| 1 |
| 2 |
解答: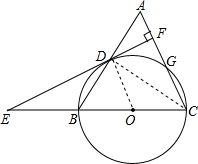 解:如图,连接OD,CD,
解:如图,连接OD,CD,
(1)∵BC为⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴∠ACD=∠BCD,
∵OC=OD,
∴∠BCD=∠ODC,
∴∠ODC=∠ACD,
∴OD∥AC,
∵DF⊥AC,
∴∠EDO=90°,
∴OD⊥EF,
∴EF与⊙O相切;
(2)∵BC为⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD=
AB=6,
∴CD=
=
=8.
 解:如图,连接OD,CD,
解:如图,连接OD,CD,(1)∵BC为⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴∠ACD=∠BCD,
∵OC=OD,
∴∠BCD=∠ODC,
∴∠ODC=∠ACD,
∴OD∥AC,
∵DF⊥AC,
∴∠EDO=90°,
∴OD⊥EF,
∴EF与⊙O相切;
(2)∵BC为⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD=
| 1 |
| 2 |
∴CD=
| BC2-BD2 |
| 102-62 |
点评:本题主要考查了圆周角定理、勾股定理、切线的判定、等腰三角形的性质及平行线的性质等知识点,关键在于运用数形结合的思想,结合相关性质定理,正确的做出辅助线,推出OD∥AC,求得OD⊥EF.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
 已知:∠AOB=60°,∠AOC=40°.
已知:∠AOB=60°,∠AOC=40°. 某小区要在一块一边靠墙的空地上修建一个矩形花园,花园的一边靠墙,另三边用长为30m的栅栏围成
某小区要在一块一边靠墙的空地上修建一个矩形花园,花园的一边靠墙,另三边用长为30m的栅栏围成 已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
 某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.
某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图. 近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题: