题目内容
17.试一试(1)根据幂的意义,观察分析,模仿填空.
①33×34=(3×3×3)×(3×3×3×3)=37
②43×44=(4×4×4)×(4×4×4×4)=4((7))
③a3×a4=a•a•a•a•a•a•a=a( )
概括:am•an=$\underset{\underbrace{(a•a•a…a)}}{()个}$×$\underset{\underbrace{(a•a•a…a)}}{()个}$=$\underset{\underbrace{(a•a•a…a)}}{()个}$=a( )
可得:am•an=a( )m、n为正整数
就是说:
同底数幂相乘,底数不变,指数相加.
(2)应用:
计算:①105×104
②a•a5•a7.
分析 (1)利用乘法和乘方的意义,得到同底数幂的乘法公式;
(2)利用同底数幂的乘法公式,进行计算.
解答 解:(1)根据幂的意义,观察分析,模仿填空.
①33×34=(3×3×3)×(3×3×3×3)=37
②43×44=( 4×4×4)×( 4×4×4×4)=4( (7))
③a3×a4=a•a•a•a•a•a•a=a(7)
概括:am•an=$\underset{\underbrace{(a•a•a…a)}}{()个}$×$\underset{\underbrace{(a•a•a…a)}}{()个}$=$\underset{\underbrace{(a•a•a…a)}}{()个}$=a( m+n )
可得:am•an=a( m+n )m、n为正整数
就是说:
同底数幂相乘,底数 不变,指数 相加.
故答案为:②4×4×4,4×4×4×4,7,③a•a•a•a•a•a•a,7,m+n,m+n,不变,相加.
(2)①105×104=10(5+4)=109;
②a•a5•a7=a1+5+7=a13.
点评 本题考查了同底数幂的乘法公式的推导和应用同底数幂的乘法公式的计算.掌握公式是关键.注意a的指数是1,做(2)②时容易漏加a的指数得到a12而出错.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
9.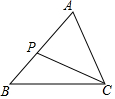 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AC}{AB}=\frac{CP}{BC}$ | D. | $\frac{AC}{AP}=\frac{AB}{AC}$ |
6.很多图标在设计时都考虑对称美.下列是几所国内知名大学的图标,若不考虑图标上的文字、字母和数字,其中是中心对称图形的是( )
| A. |  清华大学 | B. |  浙江大学 | C. |  北京大学 | D. |  中南大学 |
 如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,则△ABC中的∠C=55°.
如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,则△ABC中的∠C=55°.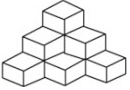 把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体,摆三层共有10个立方体,那么摆五层共有35个立方体.
把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体,摆三层共有10个立方体,那么摆五层共有35个立方体.