题目内容
12.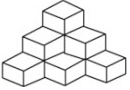 把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体,摆三层共有10个立方体,那么摆五层共有35个立方体.
把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体,摆三层共有10个立方体,那么摆五层共有35个立方体.
分析 根据题意可以得出从上到下第一层为1,第二层为1+2,…、第n层为:s=1+2+…+n,根据求和公式即可表示.
解答 解:∵第一层有1个正方体,
第二层有1+2=3个;
第三层有1+2+3=6个,
…,
第四层有1+2+3+4=10,
∴第n层有:1+2+3+…+n=$\frac{1}{2}$n(n+1)个,
当n=5时,
$\frac{1}{2}$n(n+1)=$\frac{1}{2}$×5×6=15,
共有:1+3+6+10+15,=35个,
故答案为:35.
点评 此题主要考查了图形的变化规律,根据图形得出第n层为:s=1+2+…+n是解决问题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
4.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.如图所示的操作步骤,若输入x的值为5,则输出的值为( )


| A. | 94 | B. | 95 | C. | 96 | D. | 97 |
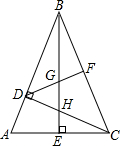 如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE
如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE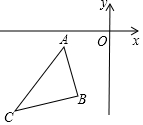 如图,在平面直角坐标系中,点A(-3,-1)、B(-2,-4)、C(-6,-5),以原点位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为(-1,-2)或(1,2).
如图,在平面直角坐标系中,点A(-3,-1)、B(-2,-4)、C(-6,-5),以原点位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为(-1,-2)或(1,2).