题目内容
5.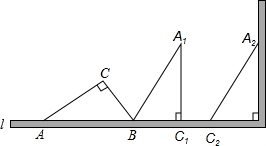 如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).(1)请直接写出AB=2米,AC=$\sqrt{3}$米;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度.
(3)设O、H分别为边AB、AC的中点,在将△ABC绕点B顺时针方向翻转到△A1BC1的位置这一过程中,求线段OH所扫过部分的面积.
分析 (1)根据直角三角形的三边关系,30°的角所对的直角边是斜边的一半,可以直接确定AB、AC.
(2)根据要求画出路径,再用弧长公式求解路径的长度.
(3)OH扫过的面积=扇形BHH′的面积-扇形BOO′的面积,由此即可计算.
解答 解:(1)∵∠CAB=30°,BC=1米
∴AB=2米,AC=$\sqrt{3}$米.
故答案为2米,$\sqrt{3}$米.
(2)A点经过的路径如图1中所示,
∵∠ABA1=180°-60°=120°,A1A2=AC=$\sqrt{3}$米
∴A点所经过的路径长=$\frac{120}{180}$•π•2+$\sqrt{3}$=$\frac{4}{3}$π+$\sqrt{3}$≈5.9(米).
(3)如图2中,
由题意△BOH≌△BO′H′,
∴OH扫过的面积=扇形BHH′的面积-扇形BOO′的面积=$\frac{120π•H{B}^{2}}{360}$-$\frac{120π•O{B}^{2}}{360}$=$\frac{1}{4}$π.
点评 本题考查旋转变换、平移变换、勾股定理.扇形的面积公式等知识,解题的关键是熟练应用所学知识解决问题,学会把不规则图形转化为规则图形,属于中考常考题型.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
13.在一定条件下,若物体运动的路程S(m)与时间t(s)的关系式为S=3t2+2t,则当t=4s时,该物体所经过的路程是( )
| A. | 56m | B. | 46m | C. | 36n | D. | 26m |
20.正数x的算术平方根是( )
| A. | x | B. | $\sqrt{x}$ | C. | ±$\sqrt{x}$ | D. | |x| |
10.下列图形的四个顶点在同一个圆上的是( )
| A. | 矩形、平行四边形 | B. | 菱形、正方形 | C. | 正方形、直角梯形 | D. | 矩形、等腰梯形 |
17.将△ABC的各边都扩大3倍,则∠A的三个三角函数值都( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 无法确定 |
14.|-$\frac{1}{2015}$|的倒数是( )
| A. | 2015 | B. | -2015 | C. | -$\frac{1}{2015}$ | D. | $\frac{1}{2015}$ |