题目内容
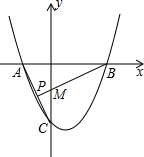 如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=
如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=| 5 |
(1)求抛物线的解析式;
(2)过点B作BP⊥AC,垂足为点P,BP交y轴于点M,求tan∠OMB.
考点:抛物线与x轴的交点
专题:
分析:(1)由条件可先求得OC的长,可求得c,再把A点坐标代入可求得b,可求得抛物线的解析式;
(2)根据题意可求是∠OMB=∠CAO,在Rt△AOC中,可求得答案.
(2)根据题意可求是∠OMB=∠CAO,在Rt△AOC中,可求得答案.
解答:
解:(1)∵OA=1,AC=
,
∴OC=
=
=2,
∴c=-2,
将(-1,0)代入y=x2-bx-2,解得b=1,
∴抛物线解析式为y=x2-x-2;
(2)∵BP⊥AC,
∴∠CAO+∠ABP=90°,
∵∠OMB+∠ABP=90°,
∴∠OMB=∠CAO,
∴tan∠OMB=tan∠CAO=
=
=2.
| 5 |
∴OC=
| AC2-OA2 |
(
|
∴c=-2,
将(-1,0)代入y=x2-bx-2,解得b=1,
∴抛物线解析式为y=x2-x-2;
(2)∵BP⊥AC,
∴∠CAO+∠ABP=90°,
∵∠OMB+∠ABP=90°,
∴∠OMB=∠CAO,
∴tan∠OMB=tan∠CAO=
| OC |
| OA |
| 2 |
| 1 |
点评:本题主要考查待定系数法求函数解析式及三角函数的定义,掌握线段的长度与相应坐标的关系是解题的关键,在(2)中注意等角的三角函数值相等是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
在以下4个数,-
,0.
,π,3.14中,无理数的个数是( )
| 3 |
| • |
| 2 |
| • |
| 1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC和△DCE中,AB∥DC,AB=DC,BC=CE,且点B,C,E在一条直线上.
如图,在△ABC和△DCE中,AB∥DC,AB=DC,BC=CE,且点B,C,E在一条直线上. 如图,B是线段AD上的一点,△ABC和△BDE都是等边三角形,连接AE、CD,点P、Q分别是AE、CD的中点,判断△PBQ的形状,并说明理由.
如图,B是线段AD上的一点,△ABC和△BDE都是等边三角形,连接AE、CD,点P、Q分别是AE、CD的中点,判断△PBQ的形状,并说明理由. 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD 如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是
如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是 如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.
如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.