题目内容
 如图,B是线段AD上的一点,△ABC和△BDE都是等边三角形,连接AE、CD,点P、Q分别是AE、CD的中点,判断△PBQ的形状,并说明理由.
如图,B是线段AD上的一点,△ABC和△BDE都是等边三角形,连接AE、CD,点P、Q分别是AE、CD的中点,判断△PBQ的形状,并说明理由.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:先根据等边三角形的性质得出AB=CB,BE=BD,∠ABC=∠DBE=60°,那么∠ABE=∠CBD,由SAS证明△ABE≌△CBD,得到AE=CD,∠EAB=∠DCB.由点P、Q分别是AE、CD的中点,得出AP=CQ.再由SAS证明△ABP≌△CBQ,然后根据等边三角形的判定定理解答即可.
解答:
解:△PBQ是等边三角形.理由如下:
∵△ABC和△BDE分别是等边三角形,
∴AB=CB,BE=BD,
∴∠ABC=∠DBE=60°,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD.
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠EAB=∠DCB.
∵点P、Q分别是AE、CD的中点,
∴AP=
AE,CQ=
CD,
∴AP=CQ.
在△ABP和△CBQ中,

,
∴△ABP≌△CBQ(SAS),
∴∠PBA=∠QBC,PB=QB,
∴∠QBP=∠QBC-∠PBC=∠PBA-∠PBC=∠ABC=60°,
∴△PBQ是等边三角形.
∵△ABC和△BDE分别是等边三角形,
∴AB=CB,BE=BD,
∴∠ABC=∠DBE=60°,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD.
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS),
∴AE=CD,∠EAB=∠DCB.
∵点P、Q分别是AE、CD的中点,
∴AP=
| 1 |
| 2 |
| 1 |
| 2 |
∴AP=CQ.
在△ABP和△CBQ中,

|
∴△ABP≌△CBQ(SAS),
∴∠PBA=∠QBC,PB=QB,
∴∠QBP=∠QBC-∠PBC=∠PBA-∠PBC=∠ABC=60°,
∴△PBQ是等边三角形.
点评:此题考查的是全等三角形、等边三角形的判定及性质,难度适中.证明出△ABE≌△CBD,进而得出得出AP=CQ是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若有理数x的相反数是8,则x为( )
| A、-8 | ||
| B、8 | ||
C、-
| ||
D、
|
在
,-
,
,π,这四个数中,无理数有( )
| 22 |
| 7 |
| 3 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
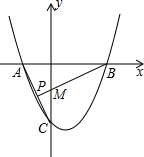 如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=
如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=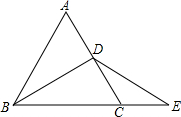 如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为
如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为