题目内容
 如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是
如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是考点:全等三角形的判定
专题:
分析:根据∠BAC=∠DAE,可证明∠BAD=∠EAC,再根据已知条件可添加一对角或加这个角的另一条边即可.
解答:
解:∵∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-CAD,即∠BAD=∠EAC,
添加AF=AH,
在△ABF和△AEH中,
,
∴△ABF≌△AEH(SAS);
添加∠B=∠E,
在△ABF和△AEH中,
,
∴△ABF≌△AEH(ASA);
添加∠AFB=∠AHE,
在△ABF和△AEH中,
,
∴△ABF≌△AEH(AAS);
故答案为AF=AH,∠B=∠E,∠AFB=∠AHE.
∴∠BAC-∠CAD=∠DAE-CAD,即∠BAD=∠EAC,
添加AF=AH,
在△ABF和△AEH中,
|
∴△ABF≌△AEH(SAS);
添加∠B=∠E,
在△ABF和△AEH中,
|
∴△ABF≌△AEH(ASA);
添加∠AFB=∠AHE,
在△ABF和△AEH中,
|
∴△ABF≌△AEH(AAS);
故答案为AF=AH,∠B=∠E,∠AFB=∠AHE.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积为( )
如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积为( )| A、15 | B、16 |
| C、18 | D、无法计算 |
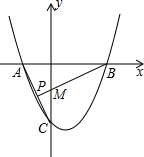 如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=
如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=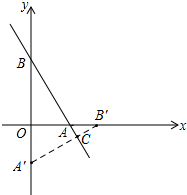 如图,直线l:y=-
如图,直线l:y=-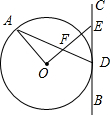 如图,已知BC与⊙O相切于点D,A为⊙O上的动点,OE⊥OA,OE分别与BC、AD交于点E、F.
如图,已知BC与⊙O相切于点D,A为⊙O上的动点,OE⊥OA,OE分别与BC、AD交于点E、F.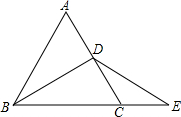 如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为
如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为