题目内容
 如图,在△ABC和△DCE中,AB∥DC,AB=DC,BC=CE,且点B,C,E在一条直线上.
如图,在△ABC和△DCE中,AB∥DC,AB=DC,BC=CE,且点B,C,E在一条直线上.求证:∠A=∠D.
考点:全等三角形的判定与性质
专题:证明题
分析:先根据平行线的性质得∠B=∠DCE,再根据“SAS”判断△ABC≌△DCE,然后根据全等三角形的性质即可得到答案.
解答:
证明:∵AB∥DC,
∴∠B=∠DCE,
在△ABC和△DCE中,
,
∴△ABC≌△DCE(SAS),
∴∠A=∠D.
∴∠B=∠DCE,
在△ABC和△DCE中,
|
∴△ABC≌△DCE(SAS),
∴∠A=∠D.
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
下列因式分解正确的是( )
| A、x2-6x+9=(x-3)2 |
| B、x2-y2=(x-y)2 |
| C、x2-5x+6=(x+1)(x-6) |
| D、6x2+2x=x(6x+2) |
 如图所示的是一长方形纸板,请你把它裁成两块,然后拼成一个正方形,你能做到吗?并说明是通过如何平移得到的.
如图所示的是一长方形纸板,请你把它裁成两块,然后拼成一个正方形,你能做到吗?并说明是通过如何平移得到的.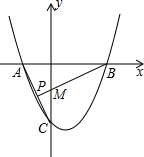 如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=
如图,抛物线y=x2-bx+c(c<0)与x轴交于A(-1,0),B两点,与y轴交于点C,AC=