题目内容
7.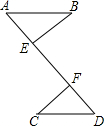 如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )| A. | AB=DC,∠B=∠C | B. | AB=DC,AB∥CD | C. | AB=DC,BE=CF | D. | AB=DF,BE=CF |
分析 根据BE⊥AD,CF⊥AD,可得∠AEB=∠CFD,然后再利用全等三角形的判定定理分别进行分析即可.
解答 解:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠CFD=90°,
选项A可利用AAS定理证明Rt△ABE≌Rt△DCF;
选项B可得∠A=∠D,可利用AAS定理证明Rt△ABE≌Rt△DCF;
选项C可利用HL定理证明Rt△ABE≌Rt△DCF;
选项D不能定理证明Rt△ABE≌Rt△DCF.
故选D.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
12.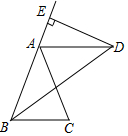 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
15.有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )


| A. | ab>0 | B. | $\frac{a}{b}>0$ | C. | a-1>0 | D. | a<b |
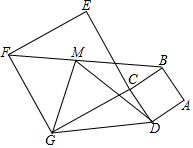 如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.
如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.