题目内容
3．
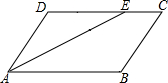如图，在?ABCD中，∠BAD的平分线AE交边CD于点E，AB=5cm，BC=3cm，则EC=2cm．
分析 直接利用角平分线的性质结合平行四边形的性质得出∠DAE=∠DEA，进而得出答案．
解答 解：∵四边形ABCD是平行四边形，
∴AB=DC=5cm，BC=AD=3cm，AB∥DC，
∴∠BAE=∠DEA，
∵∠BAD的平分线AE交边CD于点E，
∴∠DAE=∠BAE，
∴∠DAE=∠DEA，
∴AD=DE=3cm，
∴EC=DC-DE=5-3=2（cm）．
故答案为：2．
点评 此题主要考查了角平分线的性质以及平行四边形的性质，正确得出∠ADE=∠DEA是解题关键．
练习册系列答案
相关题目
13．
已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中正确的是（ ）
已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中正确的是（ ）| A． | a＞0 | B． | b＜0 | C． | c＜0 | D． | a+b+c＞0 |
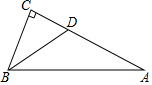如图，在△ABC中，∠C=90°，BD平分∠ABC，若BD=5，BC=4，则点D到边AB的距离为3．
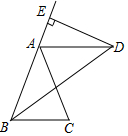如图，已知BD平分∠ABC，AB=AD，DE⊥AB，垂足为E．
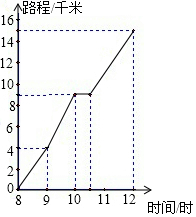图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图．根据图象回答问题：