题目内容
1. 如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G,
如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G,(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=2$\sqrt{2}$-1,求KD的长度.
分析 (1)①先根据AAS判定△DOK≌△BOG,②再根据等腰三角形ABF和平行四边形AFKG的性质,得出结论BG=AB+AK;
(2)①先根据等量代换得出AF=KG=KD=BG,再设AB=a,根据AK=FG列出关于a的方程,求得a的值,进而计算KD的长;
解答 解:(1)①∵在矩形ABCD中,AD∥BC
∴∠KDO=∠GBO,∠DKO=∠BGO
∵点O是BD的中点
∴DO=BO
在△KDO和△GBO中,
$\left\{\begin{array}{l}{∠KDO=∠GBO}\\{∠KOD=∠BOG}\\{DO=BO}\end{array}\right.$,
∴△DOK≌△BOG(AAS)
②∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AD∥BC
又∵AF平分∠BAD
∴∠BAF=∠BFA=45°
∴AB=BF
∵OK∥AF,AK∥FG
∴四边形AFGK是平行四边形
∴AK=FG
∵BG=BF+FG
∴BG=AB+AK
(2)①由(1)得,四边形AFGK是平行四边形
∴AK=FG,AF=KG
又∵△DOK≌△BOG,且KD=KG
∴AF=KG=KD=BG
设AB=a,则AF=KG=KD=BG=$\sqrt{2}$a
∴AK=2$\sqrt{2}$-1-$\sqrt{2}$a,FG=BG-BF=$\sqrt{2}$a-a
∴2$\sqrt{2}$-1-$\sqrt{2}$a=$\sqrt{2}$a-a
解得a=1,
∴KD=$\sqrt{2}$a=$\sqrt{2}$.
点评 本题主要考查了矩形的性质、平行四边形的性质、全等三角形的判定与性质等知识,解答此题的关键是学会利用参数构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.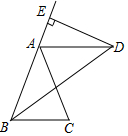 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
9.下面计算正确的是( )
| A. | (-3)2=-9 | B. | (-2)3=-8 | C. | $\sqrt{16}$=±4 | D. | -$\root{3}{-8}$=-2 |
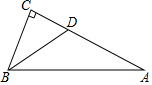 如图,在△ABC中,∠C=90°,BD平分∠ABC,若BD=5,BC=4,则点D到边AB的距离为3.
如图,在△ABC中,∠C=90°,BD平分∠ABC,若BD=5,BC=4,则点D到边AB的距离为3.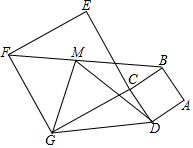 如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.
如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.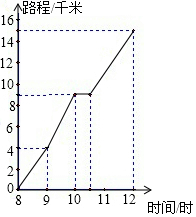 图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题:
图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题: