题目内容
20.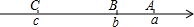 如图,已知数轴上A,B,C三点对应的数分别为a,b,c,化简|a-b|+|c-b|+|c-a|=2a-2c.
如图,已知数轴上A,B,C三点对应的数分别为a,b,c,化简|a-b|+|c-b|+|c-a|=2a-2c.
分析 根据数轴可得:a>b>c,由此可判断a-b、c-b、c-a的符号,去掉绝对值合并即可.
解答 解:由数轴可得:a>b>c,
则a-b>0,c-b<0,c-a<0,
故|a-b|+|c-b|+|c-a|
=a-b-(c-b)-(c-a)
=a-b-c+b-c+a
=2a-2c.
故答案为2a-2c.
点评 本题考查了整式的加减,解答本题的关键是判断各代数式的符号,去掉绝对值符号,难度一般.

练习册系列答案
相关题目
12.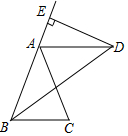 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
15.有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )


| A. | ab>0 | B. | $\frac{a}{b}>0$ | C. | a-1>0 | D. | a<b |
10.在-3,-2、0、2这四个数中,最大的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
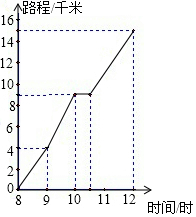 图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题:
图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题: