题目内容
12．
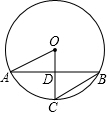如图，⊙O的半径OC垂直于弦AB，垂足为D，OA=2$\sqrt{2}$，∠B=22.5°，AB的长为（ ）| A． | 2 | B． | 4 | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
分析 根据圆周角定理，可得∠O，根据正切函数，可得AD的长，根据垂径定理，可得答案．
解答 解：由圆周角定理，得
∠O=2∠B=45°，
AD=OA•sin∠O=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2，
由垂径定理，得
AB=2AD=4，
故选：B．
点评 本题考查了垂径定理，利用圆周角定理得出∠O是解题关键，又利用了正弦函数，垂径定理．
练习册系列答案
相关题目
20．
如图，四边形ABCD是菱形，E、F、G、H分别是各边的中点，随机向菱形ABCD内部掷一粒米，则米粒落到阴影区域内的概率是（ ）
如图，四边形ABCD是菱形，E、F、G、H分别是各边的中点，随机向菱形ABCD内部掷一粒米，则米粒落到阴影区域内的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{8}$ | D． | $\frac{2}{3}$ |
如图，AB为⊙O的直径，弦BC，DE相交于点F，且DE⊥AB于点G，过点C作⊙O的切线交DE的延长线于点H．
1．某校甲、乙、丙、丁四名同学在运动会上参加4×100米接力比赛，其中甲跑第一棒，那么乙跑第二棒的概率为（ ）
| A． | $\frac{1}{24}$ | B． | $\frac{1}{12}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
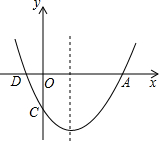如图，二次函数y=ax2+bx+c的图象与x轴的交点为A、D（A在D的右侧），与y轴的交点为C，且A（4，0），C（0，-3），对称轴是直线x=1．