题目内容
3.在等边三角形ABC中,点D、E分别在AB、BC边上,连结CD,AE交于点P,且CD=AE,∠BCD=20°,则∠APD的度数为60°或80°.分析 分两种情况进行讨论:当△ABE≌△CAD时,存在CD=AE;当△ABE≌△CBD时,存在CD=AE,分别根据三角形的外角性质以及三角形内角和定理进行计算.
解答 解:如图所示,当△ABE≌△CAD时,存在CD=AE,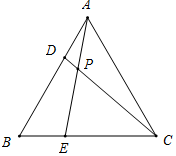
此时,∠BAE=∠ACD,
又∵∠BAE+∠CAE=60°,
∴∠ACD+∠CAE=60°,
即∠APD=60°;
如图所示,当△ABE≌△CBD时,存在CD=AE,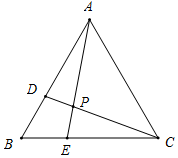
此时,∠BAE=∠BCD=20°,
∵∠B=60°,∠ADP是△BCD的外角,
∴∠ADP=60°+20°=80°,
∴△ADP中,∠APD=180°-20°-80°=80°,
综上所述,∠APD的度数为60°或80°.
故答案为:60°或80°.
点评 本题主要考查了等边三角形的性质,全等三角形的性质以及三角形外角性质的综合应用,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
11.一元二次方程x2-4x+3=0的根是( )
| A. | -1 | B. | -3 | C. | 1和3 | D. | -1和-3 |
12.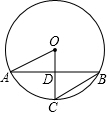 如图,⊙O的半径OC垂直于弦AB,垂足为D,OA=2$\sqrt{2}$,∠B=22.5°,AB的长为( )
如图,⊙O的半径OC垂直于弦AB,垂足为D,OA=2$\sqrt{2}$,∠B=22.5°,AB的长为( )
 如图,⊙O的半径OC垂直于弦AB,垂足为D,OA=2$\sqrt{2}$,∠B=22.5°,AB的长为( )
如图,⊙O的半径OC垂直于弦AB,垂足为D,OA=2$\sqrt{2}$,∠B=22.5°,AB的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
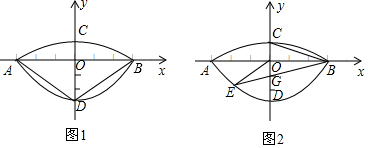
 如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是∠ABC=90°(只需添加一个即可)
如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是∠ABC=90°(只需添加一个即可) 高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题: