Question

6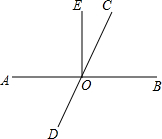．如图，已知AB，CD相交于点O，OE平分∠AOB，∠EOC=28°．
（1）求∠AOC和∠AOD的度数；
（2）判断∠AOD与∠COB的大小关系．并说明理由．

Answer 1

分析 （1）根据两直线相交可得∠AOB=∠COD=180°，由OE平分∠AOB，知∠AOE=∠BOE=90°，于是∠AOC=90°+∠EOC，∠AOD=180°-∠AOC，代入可得结果；
（2）由于∠BOC与∠AOD是对顶角，根据对顶角的性质可得相等．

解答 解：（1）∵直线AB、CD相交于点O，
∴∠AOB=∠COD=180°，
∵OE平分∠AOB，
∴∠AOE=∠BOE=90°，
∴∠AOC=90°+∠EOC=90°+28°=118°，
，∠AOD=180°-∠AOC=180°-118°=62°；

（2）∠AOD=∠COB，
∵∠BOC与∠AOD是对顶角，
∴∠BOC=∠AOD．

点评 本题考查了对顶角的性质及角平分线的性质，熟练掌握性质是解题的关键．