题目内容
19. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.(1)求证:∠BCO=∠D;
(2)若CD=8,AE=3,求⊙O的半径.
分析 (1)由等腰三角形的性质与圆周角定理,易得∠BCO=∠B=∠D;
(2)由垂径定理可求得CE与DE的长,然后证得△BCE∽△DAE,再由相似三角形的对应边成比例,求得BE的长,继而求得直径与半径.
解答 (1)证明:∵OB=OC,
∴∠BCO=∠B,
∵∠B=∠D,
∴∠BCO=∠D;
(2)解:∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=$\frac{1}{2}$×8=4,
∵∠B=∠D,∠BEC=∠DEC,
∴△BCE∽△DAE,
∴AE:CE=DE:BE,
∴3:4=4:BE,
解得:BE=$\frac{16}{3}$,
∴AB=AE+BE=$\frac{25}{3}$,
∴⊙O的半径为:$\frac{25}{6}$.
点评 此题考查了圆周角定理、垂径定理、相似三角形的判定与性质以及等腰三角形的性质.注意在同圆或等圆中,同弧或等弧所对的圆周角相等.证得△BCE∽△DAE是关键.

练习册系列答案
相关题目
9.如果a,b互为相反数,那么(6a2-12a)-6(a2+2b-5)的值为( )
| A. | -18 | B. | 18 | C. | 30 | D. | -30 |
7.2015年6月份我省农产品实现出口额7312万美元,其中7312万用科学记数法表示为( )
| A. | 0.7312×108 | B. | 7.312×108 | C. | 7.312×107 | D. | 73.12×106 |
14.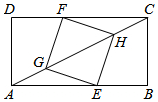 如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | $\frac{9}{2}$ | D. | $\frac{25}{4}$ |
 如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形.
如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形.