题目内容
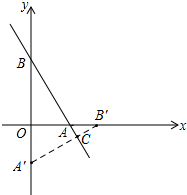 如图,直线l:y=-
如图,直线l:y=-| 4 |
| 3 |
(1)求A′、B′两点的坐标及直线A′B′的解析式.
(2)求△A′BC的面积.
考点:待定系数法求一次函数解析式,坐标与图形变化-旋转
专题:
分析:(1)先根据一次函数的解析式求出AB两点的坐标,再由图形旋转的性质求出A′、B′的坐标,用待定系数法求出直线A′B′的解析式即可;
(2)直接根据A′、B、C的坐标,利用三角形的面积公式进行计算即可.
(2)直接根据A′、B、C的坐标,利用三角形的面积公式进行计算即可.
解答:
解:(1)∵令x=0,则y=4,令y=0,则x=3,
∴A(3,0),B(0,4),
由图形旋转的性质可知,A′( 0,-3),B′( 4,0),
设过A′( 0,-3),B′( 4,0)的解析式为y=kx+b(k≠0)
则
,
解得
.
故此直线的解析式为:y=
x-3;
(2)∵过A′,B′两点的解析式为:y=
x-3,
∴
,
解得
,
∴C(
,-
),
∴S△A’BC=
|A′B|×xC=
×7×
=
.
∴A(3,0),B(0,4),
由图形旋转的性质可知,A′( 0,-3),B′( 4,0),
设过A′( 0,-3),B′( 4,0)的解析式为y=kx+b(k≠0)
则
|
解得
|
故此直线的解析式为:y=
| 3 |
| 4 |
(2)∵过A′,B′两点的解析式为:y=
| 3 |
| 4 |
∴
|
解得
|
∴C(
| 84 |
| 25 |
| 12 |
| 25 |
∴S△A’BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 84 |
| 25 |
| 294 |
| 25 |
点评:本题考查的是一次函数的图象与及几何变换、一次函数的性质及三角形的面积公式,根据题意求出直线A′B′的解析式是解答此题的关键.

练习册系列答案
相关题目
用直接开平方法解方程(x+m)2=n,下列结论正确的是( )
A、有两个根,为x=±
| ||
B、当n>0时,有两个根,为x=±
| ||
C、当x>0时,有两个根,为x=±
| ||
| D、当n<0时,无实数根 |
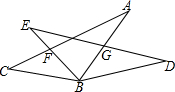 如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )
如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )| A、∠A=∠D |
| B、BF=BG |
| C、AC=DE |
| D、BA=BD |
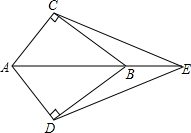 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD 如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是
如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是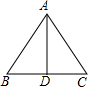 如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是
如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是 在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.
在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.