题目内容
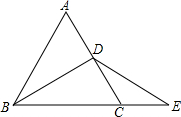 如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为
如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为考点:等边三角形的性质,等腰三角形的性质
专题:
分析:先根据等边三角形的三线合一性质求出CD,再根据勾股定理求出BD,然后再证出CE=CD即可得出结论.
解答:
解:∵△ABC是等边三角形,
∴BC=AC=6,∠ABC=∠ACB=60°,
D为AC的中点,
∴∠CBD=30°,CD=
AC=3,
∴BD=
=3
,
∵DB=DE=3
,
∴∠DEC=∠CBD=30°,
∴∠CDE=60°-30°=30°,
∴∠E=∠CDE,
∴CE=CD=3,
∴△DCE的周长为:DE+CD+CE=3
+3+3=3
+6;
故答案为:3
+6.
∴BC=AC=6,∠ABC=∠ACB=60°,
D为AC的中点,
∴∠CBD=30°,CD=
| 1 |
| 2 |
∴BD=
| 62-32 |
| 3 |
∵DB=DE=3
| 3 |
∴∠DEC=∠CBD=30°,
∴∠CDE=60°-30°=30°,
∴∠E=∠CDE,
∴CE=CD=3,
∴△DCE的周长为:DE+CD+CE=3
| 3 |
| 3 |
故答案为:3
| 3 |
点评:本题考查了等边三角形的性质和等腰三角形的性质与判定;熟练掌握等边三角形和等腰三角形的性质是解决问题的关键.

练习册系列答案
相关题目
 如图,B是线段AD上的一点,△ABC和△BDE都是等边三角形,连接AE、CD,点P、Q分别是AE、CD的中点,判断△PBQ的形状,并说明理由.
如图,B是线段AD上的一点,△ABC和△BDE都是等边三角形,连接AE、CD,点P、Q分别是AE、CD的中点,判断△PBQ的形状,并说明理由. 如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是
如图,AB=AE,∠BAC=∠DAE,要使△ABF≌△AEH,还需添加的条件是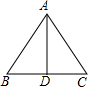 如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是
如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是 在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.
在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.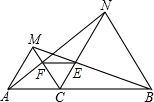 如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.
如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形. 如图,在△ABC中,∠C=90°,点E是斜边AB的中点,DE⊥AB,且∠CAD:∠BAD=5:2,求∠BAC的度数.
如图,在△ABC中,∠C=90°,点E是斜边AB的中点,DE⊥AB,且∠CAD:∠BAD=5:2,求∠BAC的度数.